题目内容
若直角三角形的两条直角边各扩大一倍，则斜边（ ）
| A、不变 | B、扩大一倍 |
| C、扩大两倍 | D、扩大四倍 |
考点：勾股定理
专题：
分析：根据勾股定理求出扩大后斜边的长度，与原斜边长度比较即可得出答案．
解答：解：设一直角三角形直角边为a、b，斜边为c，则a2+b2=c2；
扩大2倍后，直角三角形直角边为2a、2b，则根据勾股定理知斜边为：
=2c．
即直角三角形两直角边同时扩大到原来的2倍，则斜边扩大到原来的2倍．
故选C．
扩大2倍后，直角三角形直角边为2a、2b，则根据勾股定理知斜边为：
| (2a)2+(2b)2 |
即直角三角形两直角边同时扩大到原来的2倍，则斜边扩大到原来的2倍．
故选C．
点评：此题考查了勾股定理的知识，属于基础题，解答本题关键是利用勾股定理求出扩大后斜边的长度，难度一般．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，P是正方形ABCD内一点，将△ABP绕点B按顺时针旋转90°到△CBP′，若PB=
如图，△ABC的三个顶点A（-3，-2）、B（-1，-3）、C（-2，0）．以原点O为位似中心，将△ABC缩小，使变换后得到△DEF与△ABC的位似比为1：2，那么顶点A的对应点D′的坐标为（ ）| A、（-1，-1） | ||||
| B、（1，-1） | ||||
C、（-
| ||||
| D、（-1，-1）或（1，1） |
已知，如图∠1=∠2，BF=EC，AC=DF．求证：△ABC≌△DEF．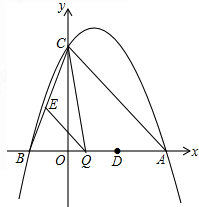
已知，如图，抛物线y=ax2-2ax+c（a≠0）与y轴交于点C（0，3），与x轴交于点A、B，点A的坐标为（3，0），点O为坐标原点．