Question

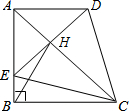如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=BC，E为AB边上一点，∠BCE=15°，且AE=AD．连接DE交对角线AC于H，连接BH．下列结论：
①△ACD≌△ACE；②△CDE为等边三角形；③EH=2EB；④

S△AEH

S△CEH

=

EH

CD

．
其中正确的结论是

 

．

Answer 1

考点：直角梯形,全等三角形的判定与性质,等边三角形的判定,勾股定理

专题：

分析：由∠ABC=90°，AB=BC，易证得△ACD≌△ACE；由∠BCE=15°，易求得∠DEC=60°，继而可证得△CDE为等边三角形；由△CHE为直三角形，且∠HEC=60°可得EC=2EH，又由∠ECB=15°，可得EC≠4EB，即可得EH≠2EB；易证得

S△AEH

S△CEH

＞

EH

CD

．

解答：解：①∵∠ABC=90°，AB=BC，
∴∠BAC=∠ACB=45°，
又∵∠BAD=90°，
∴∠BAC=∠DAC，
在△ACD和△ACE中，

AD=AE ∠EAC=∠DAC AC=AC

，
∴△ACD≌△ACE（SAS）；故①正确；

②同理∠AED=45°，∠BEC=90°-∠BCE=90°-15°=75°，
∴∠DEC=60°，
∵△ACD≌△ACE，
∴CD=CE，
∴△CDE为等边三角形．故②正确．

③∵△CHE为直角三角形，且∠HEC=60°
∴EC=2EH
∵∠ECB=15°，
∴EC≠4EB，
∴EH≠2EB；故③错误．

④∵AE=AD，CE=CD，
∴点A与C在DE的垂直平分线上，
∴AC是DE的垂直平分线，
即AC⊥DE，
∴CE＞CH，
∵CD=CE，
∴CD＞CH，
∵∠BAC=45°，
∴AH=EH，
∵

S△AEH

S△CEH

=

AH

CH

，
∴

S△AEH

S△CEH

＞

EH

CD

，故④错误．
故答案为：①②．

点评：此题考查了直角梯形的性质、全等三角形的判定与性质、等边三角形的判定与性质以及等腰直角三角形性质．此题难度较大，注意掌握数形结合思想的应用．