题目内容
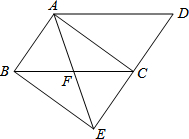 如图,将平行四边形ABCD的边DC延长至点E,使CE=DC,连接AE,交BC于点F.
如图,将平行四边形ABCD的边DC延长至点E,使CE=DC,连接AE,交BC于点F.(1)求证:△ABF≌△ECF;
(2)连接AC、BE,则当∠AFC与∠D满足什么条件时,四边形ABEC是矩形?请说明理由.
考点:矩形的判定,全等三角形的判定与性质,平行四边形的性质
专题:
分析:(1)由四边形ABCD是平行四边形,CE=DC,易证得∠ABF=∠ECF,∠AFB=∠EFC,AB=EC,则可证得△ABF≌△ECF;
(2)首先根据四边形ABCD是平行四边形,得到四边形ABEC是平行四边形,然后证得FC=FE,利用对角线互相相等的四边形是矩形判定四边形ABEC是矩形.
(2)首先根据四边形ABCD是平行四边形,得到四边形ABEC是平行四边形,然后证得FC=FE,利用对角线互相相等的四边形是矩形判定四边形ABEC是矩形.
解答:解:(1)证明:在平行四边形ABCD中,AB∥CD,AB=CD,
∴∠BAE=∠AEC,
又∵CE=CD,
∴AB=CE,
在△ABF和△ECF中,
,
∴△ABF≌△ECF(AAS);
(2)当∠AFC=2∠D时,四边形ABEC是矩形.
∵四边形ABCD是平行四边形,
∴BC∥AD,∠BCE=∠D,
由题意易得AB∥EC,AB∥EC,
∴四边形ABEC是平行四边形.
∵∠AFC=∠FEC+∠BCE,
∴当∠AFC=2∠D时,则有∠FEC=∠FCE,
∴FC=FE,
∴四边形ABEC是矩形.
∴∠BAE=∠AEC,
又∵CE=CD,
∴AB=CE,
在△ABF和△ECF中,
|
∴△ABF≌△ECF(AAS);
(2)当∠AFC=2∠D时,四边形ABEC是矩形.
∵四边形ABCD是平行四边形,
∴BC∥AD,∠BCE=∠D,
由题意易得AB∥EC,AB∥EC,
∴四边形ABEC是平行四边形.
∵∠AFC=∠FEC+∠BCE,
∴当∠AFC=2∠D时,则有∠FEC=∠FCE,
∴FC=FE,
∴四边形ABEC是矩形.
点评:此题考查了平行四边形的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
下列变形是分解因式的是( )
| A、6x2y2=3xy•2xy |
| B、m2-4=(m+2)(m-2) |
| C、a2-b2+1=(a+b)(a-b)+1 |
| D、(a+3)(a-3)=a2-9 |
 如图,平行四边形ABCD中,过对角线BD上一点P做EF∥BC,GH∥AB,关于四边形AEPG与四边形PHCF面积说法正确的是( )
如图,平行四边形ABCD中,过对角线BD上一点P做EF∥BC,GH∥AB,关于四边形AEPG与四边形PHCF面积说法正确的是( )| A、四边形AEPG大 |
| B、四边形PHCF大 |
| C、一样大 |
| D、无法确定 |
 如图,直线AB∥CD∥EF,且∠ABE=70°,∠ECD=150°,则∠BEC=( )
如图,直线AB∥CD∥EF,且∠ABE=70°,∠ECD=150°,则∠BEC=( )| A、50° | B、30° |
| C、20° | D、40° |
 如图,在直角△ABC中,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交BC于点E,连接AE,则△ACE的周长为( )
如图,在直角△ABC中,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交BC于点E,连接AE,则△ACE的周长为( ) 已知:如图,CD∥EF,∠1=65°,∠2=35°,求∠3与∠4的度数.
已知:如图,CD∥EF,∠1=65°,∠2=35°,求∠3与∠4的度数. 如图,四边形ABCD中,CD⊥AD,CB⊥AB,AB=AD,求证:CD=CB.
如图,四边形ABCD中,CD⊥AD,CB⊥AB,AB=AD,求证:CD=CB.