题目内容
如图，在直角△ABC中，∠BAC=90°，AB=8，AC=6，DE是AB边的垂直平分线，垂足为D，交BC于点E，连接AE，则△ACE的周长为（ ）| A、16 | B、15 | C、14 | D、13 |
考点：线段垂直平分线的性质,勾股定理
专题：
分析：由DE是AB边的垂直平分线，可得AE=BE，又由在直角△ABC中，∠BAC=90°，AB=8，AC=6，利用勾股定理即可求得BC的长，继而由△ACE的周长=AC+BC，求得答案．
解答：解：∵DE是AB边的垂直平分线，
∴AE=BE，
∵在直角△ABC中，∠BAC=90°，AB=8，AC=6，
∴BC=
=
=10，
∴△ACE的周长为：AC+AE+CE=AC+BE+CE=AC+BC=6+10=16．
故选A．
∴AE=BE，
∵在直角△ABC中，∠BAC=90°，AB=8，AC=6，
∴BC=
| AB2+AC2 |
| 82+62 |
∴△ACE的周长为：AC+AE+CE=AC+BE+CE=AC+BC=6+10=16．
故选A．
点评：此题考查了线段垂直平分线的性质以及勾股定理．此题难度不大，注意掌握数形结合思想与转化思想的应用．
练习册系列答案
相关题目
如图，AB∥CD，则与∠1相等的角（∠1除外）共有方程3x+2y=8的正整数解有（ ）
| A、1组 | B、2组 | C、3组 | D、4组 |
计算（ab2）（-3a2b）2的结果是（ ）
| A、6a5b4 |
| B、-6a5b4 |
| C、9a5b4 |
| D、9a3b4 |
下列长度的三条线段中，能组成三角形的是（ ）
| A、3，5，8 |
| B、8，8，18 |
| C、0.1，0.1，0.1 |
| D、3，40，8 |
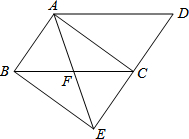如图，将平行四边形ABCD的边DC延长至点E，使CE=DC，连接AE，交BC于点F．