题目内容
4.阅读下列材料:如图1,在线段AB上找一点C(AC>BC),若BC:AC=AC:AB,则称点C为线段AB的黄金分割点,这时比值为$\frac{\sqrt{5}-1}{2}$≈0.618,人们把$\frac{\sqrt{5}-1}{2}$称为黄金分割数.长期以来,很多人都认为黄金分割数是一个很特别的数,我国著名数学家华罗庚先生所推广的优选法中,就有一种0.618法应用了黄金分割数.
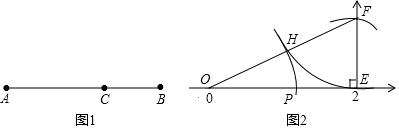
我们可以这样作图找到已知线段的黄金分割点:如图2,在数轴上点O表示数0,点E表示数2,过点E作EF⊥OE,且EF=$\frac{1}{2}$OE,连接OF;以F为圆心,EF为半径作弧,交OF于H;再以O为圆心,OH为半径作弧,交OE于点P,则点P就是线段OE的黄金分割点.
根据材料回答下列问题:
(1)线段OP长为$\sqrt{5}-1$,点P在数轴上表示的数为$\sqrt{5}$-1;
(2)在(1)中计算线段OP长的依据是勾股定理.
分析 (1)根据勾股定理得到OF=$\sqrt{O{E}^{2}+E{F}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,根据线段的和差即可得到结论;
(2)根据勾股定理求得OF,再由线段的和差求得OP,于是得到结论.
解答 解:(1)∵OE=2,
∴EF=$\frac{1}{2}$OE=1,
∵EF⊥OE,
∴OF=$\sqrt{O{E}^{2}+E{F}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
由作法知,FH=EF=1,OP=OH=OF-FH=$\sqrt{5}$-1,
∴点P在数轴上表示的数为:$\sqrt{5}$-1,
故答案为:$\sqrt{5}$-1,$\sqrt{5}$-1;
(2)在(1)中计算线段OP长时,
首先根据勾股定理求得OF,
再由OP=OH=OF-FH求得OP,
故答案为:勾股定理.
点评 本题考查了黄金分割,勾股定理,熟练掌握勾股定理是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
14.因式分解x3-2x2+x正确的是( )
| A. | (x-1)2 | B. | x (x-1)2 | C. | x( x2-2x+1) | D. | x (x+1)2 |
15.已知甲、乙两数的和是6,甲数是乙数的3倍,设甲数为x,乙数为y,根据题意,列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=6}\\{x=3y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=6}\\{y=3x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+2y=6}\\{x=3y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=6}\\{y=3x}\end{array}\right.$ |
12. 如图,在?ABCD中,O是AC,BD的交点,过点O与AC垂直的直线交边AD于点E,若?ABCD的周长20厘米,则△CDE的周长为( )
如图,在?ABCD中,O是AC,BD的交点,过点O与AC垂直的直线交边AD于点E,若?ABCD的周长20厘米,则△CDE的周长为( )
 如图,在?ABCD中,O是AC,BD的交点,过点O与AC垂直的直线交边AD于点E,若?ABCD的周长20厘米,则△CDE的周长为( )
如图,在?ABCD中,O是AC,BD的交点,过点O与AC垂直的直线交边AD于点E,若?ABCD的周长20厘米,则△CDE的周长为( )| A. | 6厘米 | B. | 8厘米 | C. | 10厘米 | D. | 12厘米 |
19.按如图所示的程序计算,若开始输入n的值为1,则最后输出的结果是( )

| A. | 3 | B. | 42 | C. | 15 | D. | 63 |
16.在一个不透明的盒子中装有8个白球和若干个黄球,它们除颜色不同外,其余都相同,若从中随机摸出一个球,它是黄球的概率为$\frac{2}{3}$,则黄球的个数为( )
| A. | 4个 | B. | 6个 | C. | 12个 | D. | 16个 |
13.下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(环) | 8.9 | 9.1 | 8.9 | 9.1 |
| 方差 | 3.3 | 3.8 | 3.8 | 3.3 |
| A. | 丁 | B. | 丙 | C. | 乙 | D. | 甲 |
14.下列计算中,正确的是( )
| A. | (xy)3=xy3 | B. | (2xy)3=6x3y3 | C. | (-3x2)3=27x5 | D. | (a2b)n=a2nbn |
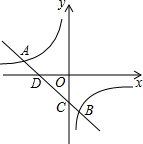 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-3,1),B(2,n)两点,交x轴、y轴于D、C两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-3,1),B(2,n)两点,交x轴、y轴于D、C两点.