题目内容
16.在一个不透明的盒子中装有8个白球和若干个黄球,它们除颜色不同外,其余都相同,若从中随机摸出一个球,它是黄球的概率为$\frac{2}{3}$,则黄球的个数为( )| A. | 4个 | B. | 6个 | C. | 12个 | D. | 16个 |
分析 设黄球的个数为x,根据概率=所求情况数与总情况数之比,列出算式,求出x的值即可得出答案.
解答 解:设黄球的个数为x,根据题意得:
$\frac{x}{8+x}$=$\frac{2}{3}$,
解得:x=16,
答:黄球的个数为16个;
故选D.
点评 此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
7.在实数4$\frac{2}{3}$,-$\root{3}{9}$,$\frac{π}{3}$,$\sqrt{10}$,0.010 010 001 000 01中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.关于x的一元二次方程x2-6x+k=0有两个不相等的实数根,则实数k的取值范围是( )
| A. | k≤9 | B. | k<9 | C. | k≥9 | D. | k>9 |
5. 如图,某小区有一块长为18m,宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为60m2,两块绿地之间及周边留有宽度相等的人形通道,若设人形道的宽度为xm,则可以列出关于x的方程是( )
如图,某小区有一块长为18m,宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为60m2,两块绿地之间及周边留有宽度相等的人形通道,若设人形道的宽度为xm,则可以列出关于x的方程是( )
 如图,某小区有一块长为18m,宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为60m2,两块绿地之间及周边留有宽度相等的人形通道,若设人形道的宽度为xm,则可以列出关于x的方程是( )
如图,某小区有一块长为18m,宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为60m2,两块绿地之间及周边留有宽度相等的人形通道,若设人形道的宽度为xm,则可以列出关于x的方程是( )| A. | x2+9x-8=0 | B. | x2-9x+8=0 | C. | x2-9x-8=0 | D. | 2x2-9x+8=0 |
6.若$\sqrt{x-3}$在实数范围内有意义,则x的取值范围是( )
| A. | x>0 | B. | x>3 | C. | x≤3 | D. | x≥3 |
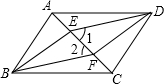 (1)如图,四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接ED,BF.求证:∠1=∠2.
(1)如图,四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接ED,BF.求证:∠1=∠2.
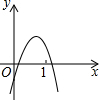 y=ax2+bx+c的图象如图所示,则下面结论中正确的结论有( )
y=ax2+bx+c的图象如图所示,则下面结论中正确的结论有( )