题目内容
在平面直角坐标系中,已知抛物线y=-
x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,-1),C的坐标为(4,3),直角顶点B在第四象限.
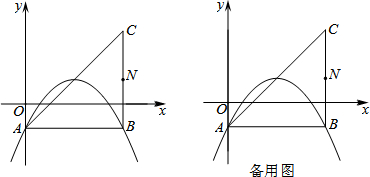
(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q,取BC的中点N,连接NP,BQ,试探究
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
| 1 |
| 2 |

(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q,取BC的中点N,连接NP,BQ,试探究
| PQ |
| NP+BQ |
考点:二次函数综合题
专题:
分析:(1)先求出点B的坐标,然后利用待定系数法求出抛物线的函数表达式;
(2)易得PQ=2
为定值,因此当NP+BQ取最小值时,
有最大值.如答图2所示,作点B关于直线AC的对称点B′,由分析可知,当B′、Q、F(AB中点)三点共线时,NP+BQ最小,最小值为线段B′F的长度.
(2)易得PQ=2
| 2 |
| PQ |
| NP+BQ |
解答:解:(1)∵等腰直角三角形ABC的顶点A的坐标为(0,-1),C的坐标为(4,3)
∴点B的坐标为(4,-1).
∵抛物线过A(0,-1),B(4,-1)两点,
∴
,
解得:b=2,c=-1,
∴抛物线的函数表达式为:y=-
x2+2x-1.
(2)
存在最大值.理由如下:
易知PQ=2
为定值,则当NP+BQ取最小值时,
有最大值.
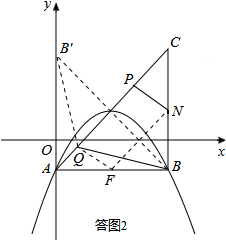
如答图2,取点B关于AC的对称点B′,易得点B′的坐标为(0,3),BQ=B′Q.
连接QF,FN,QB′,易得FN∥PQ,且FN=PQ,
∴四边形PQFN为平行四边形.
∴NP=FQ.
∴NP+BQ=FQ+B′Q≥FB′=
=2
.
∴当B′、Q、F三点共线时,NP+BQ最小,最小值为2
.
∴
的最大值为
=
.
∴点B的坐标为(4,-1).
∵抛物线过A(0,-1),B(4,-1)两点,
∴
|
解得:b=2,c=-1,
∴抛物线的函数表达式为:y=-
| 1 |
| 2 |
(2)
| PQ |
| NP+BQ |
易知PQ=2
| 2 |
| PQ |
| NP+BQ |

如答图2,取点B关于AC的对称点B′,易得点B′的坐标为(0,3),BQ=B′Q.
连接QF,FN,QB′,易得FN∥PQ,且FN=PQ,
∴四边形PQFN为平行四边形.
∴NP=FQ.
∴NP+BQ=FQ+B′Q≥FB′=
| 22+42 |
| 5 |
∴当B′、Q、F三点共线时,NP+BQ最小,最小值为2
| 5 |
∴
| PQ |
| NP+BQ |
2
| ||
2
|
| ||
| 5 |
点评:本题为二次函数中考压轴题,考查了二次函数的图象与性质、待定系数法、一次函数、几何变换(平移,对称)、等腰直角三角形、平行四边形、轴对称-最短路线问题等知识点,考查了存在型问题和分类讨论的数学思想,试题难度较大.

练习册系列答案
相关题目
 已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AC=6,BD=8,则OE的长为
已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AC=6,BD=8,则OE的长为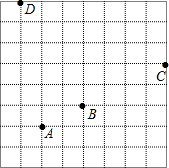 如图,是一个规格为8×8的球桌,小明用A球撞击B球,到C处反弹,再撞击桌边D处,请选择适当的平面直角坐标系,并用坐标表示各点的位置.
如图,是一个规格为8×8的球桌,小明用A球撞击B球,到C处反弹,再撞击桌边D处,请选择适当的平面直角坐标系,并用坐标表示各点的位置.
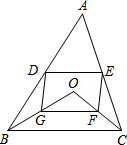 如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC平面上的一动点,连接OB、OC,G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC平面上的一动点,连接OB、OC,G、F分别是OB、OC的中点,顺次连接点D、G、F、E. 如图,抛物线y=x2沿直线y=x向上平移
如图,抛物线y=x2沿直线y=x向上平移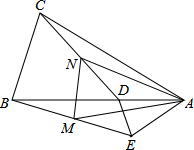 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点,下列结论:
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点,下列结论: