题目内容
20.用你发现的规律解答下列问题.$\frac{1}{1×2}$=1-$\frac{1}{2}$;$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$;$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$;…
(1)计算$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$+$\frac{1}{5×6}$=$\frac{5}{6}$.
(2)探究$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$=$\frac{n}{n+1}$.(用含有n的式子表示)
(3)若 $\frac{1}{1×4}$+$\frac{1}{4×7}$+$\frac{1}{7×10}$+…+$\frac{1}{(3n-2)(3n+1)}$的值为$\frac{15}{46}$,求n的值.
分析 (1)仿照题中的规律将原式变形,计算即可得到结果;
(2)归纳总结得到一般性规律,写出即可;
(3)根据题意列出方程,利用得出的规律变形,计算即可求出n的值.
解答 解:(1)原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{6}$=1-$\frac{1}{6}$=$\frac{5}{6}$;
(2)根据题意得:原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$;
(3)根据题意得:$\frac{1}{3}$(1-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{7}$+…+$\frac{1}{3n-2}$-$\frac{1}{3n+1}$)=$\frac{15}{46}$,即$\frac{1}{3}$(1-$\frac{1}{3n+1}$)=$\frac{15}{46}$,
解得:n=15.
故答案为:(1)$\frac{5}{6}$;(2)$\frac{n}{n+1}$
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.某校准备组织520名学生进行野外考察活动,行李共有240件.学校计划租用甲、乙两种型号的汽车共12辆,经了解,甲种汽车每辆最多能载50人和15件行李,乙种汽车每辆最多能载40人和25件行李.设租用甲种汽车x辆,你认为下列符合题意的不等式组是( )
| A. | $\left\{\begin{array}{l}{50x+40(12-x)≥520}\\{15x+25(12-x)≥240}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{50x+40(12-x)>520}\\{15x+25(12-x)>240}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{50x+40(12-x)≤520}\\{15x+25(12-x)≤240}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{50x+40(12-x)<520}\\{15x+25(12-x)<240}\end{array}\right.$ |
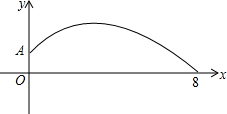 某学校在一次投掷铅球时,刚出手时铅球离地面$\frac{5}{3}$m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图所示:
某学校在一次投掷铅球时,刚出手时铅球离地面$\frac{5}{3}$m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图所示: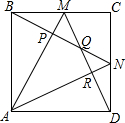 如图,M、N是单位正方形ABCD边BC、CD的中点,连接AM、DM、AN、BN,则这些线段所围成的四边形APQR的面积是$\frac{4}{15}$.
如图,M、N是单位正方形ABCD边BC、CD的中点,连接AM、DM、AN、BN,则这些线段所围成的四边形APQR的面积是$\frac{4}{15}$.