题目内容
20.下列各数是无理数的是( )| A. | 0 | B. | 2 | C. | -3 | D. | $\sqrt{2}$ |
分析 无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项
解答 解:A、0是整数,是有理数,选项不符合题意;
B、2是整数,是有理数,选项不符合题意;
C、-3是整数,是有理数,选项不符合题意;
D、$\sqrt{2}$是无理数,选项符合题意.
故选D.
点评 此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
8.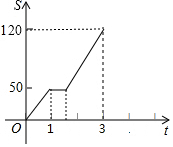 小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )
小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )
 小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )
小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )| A. | 0.5小时 | B. | 0.6小时 | C. | 0.7小时 | D. | 0.8小时 |
15.2017年春节黄金周宜春市共接待游客2234000人次,将2234000用科学记数法表示为( )
| A. | 22.34×105 | B. | 2.234×105 | C. | 2.234×106 | D. | 0.2234×107 |
12.对于问题:证明不等式a2+b2≥2ab,甲、乙两名同学的作业如下:
甲:根据一个数的平方是非负数可知(a-b)2≥0,
∴a2-2ab+b2≥0,
∴a2+b2≥2ab.
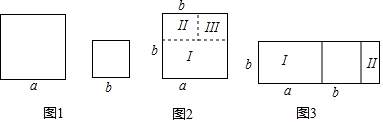
乙:如图1,两个正方形的边长分别为a、b(b≤a),如图2,先将边长为a的正方形沿虚线部分分别剪成Ⅰ、Ⅱ、Ⅲ三部分,若再将Ⅰ、Ⅱ和边长为b的正方形拼接成如图3所示的图形,可知此时图3的面积为2ab,其面积小于或等于原来两个正方形的面积和,故不等式a2+b2≥2ab成立.
则对于两人的作业,下列说法正确的是( )
甲:根据一个数的平方是非负数可知(a-b)2≥0,
∴a2-2ab+b2≥0,
∴a2+b2≥2ab.
乙:如图1,两个正方形的边长分别为a、b(b≤a),如图2,先将边长为a的正方形沿虚线部分分别剪成Ⅰ、Ⅱ、Ⅲ三部分,若再将Ⅰ、Ⅱ和边长为b的正方形拼接成如图3所示的图形,可知此时图3的面积为2ab,其面积小于或等于原来两个正方形的面积和,故不等式a2+b2≥2ab成立.
则对于两人的作业,下列说法正确的是( )

| A. | 甲、乙都对 | B. | 甲对,乙不对 | C. | 甲不对,乙对 | D. | 甲、乙都不对 |
10. 如图,直线m∥n.若∠1=70°,∠2=25°,则∠A等于( )
如图,直线m∥n.若∠1=70°,∠2=25°,则∠A等于( )
 如图,直线m∥n.若∠1=70°,∠2=25°,则∠A等于( )
如图,直线m∥n.若∠1=70°,∠2=25°,则∠A等于( )| A. | 30° | B. | 35° | C. | 45° | D. | 55° |
 如图中的四边形均为矩形,根据图形,利用图中的字母,写出一个正确的等式:(m+n)(a+b)=ma+mb+na+nb(答案不唯一).
如图中的四边形均为矩形,根据图形,利用图中的字母,写出一个正确的等式:(m+n)(a+b)=ma+mb+na+nb(答案不唯一).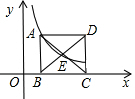 已知点(1,3)在函数y=$\frac{k}{x}$(x>0)的图象上,正方形ABCD的边BC在x轴上,点E是对角线AC、BD的交点,函数y=$\frac{k}{x}$(x>0)的图象又经过A、E两点,则点E的坐标为($\sqrt{6}$,$\frac{\sqrt{6}}{2}$).
已知点(1,3)在函数y=$\frac{k}{x}$(x>0)的图象上,正方形ABCD的边BC在x轴上,点E是对角线AC、BD的交点,函数y=$\frac{k}{x}$(x>0)的图象又经过A、E两点,则点E的坐标为($\sqrt{6}$,$\frac{\sqrt{6}}{2}$).