题目内容
当分式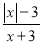 的值为0时,x的值为( )
的值为0时,x的值为( )
A. 0 B. 3 C. -3 D. ±3
 B
【解析】分式的值为0,则分子为0,分母不为0,列方程组即可求解.
【解析】
根据题意得, ,
解得,x=3;
故选B.
B
【解析】分式的值为0,则分子为0,分母不为0,列方程组即可求解.
【解析】
根据题意得, ,
解得,x=3;
故选B.
练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
982+(a-b)2
 9604+a2-2ab+b2
【解析】试题分析:把98化为(100-2),利用完全平方公式即可解答.
试题解析:
982+(a-b)2=(100-2)2+a2-2ab+b2=10000-400+4+a2-2ab+b2=9604+a2-2ab+b2.
9604+a2-2ab+b2
【解析】试题分析:把98化为(100-2),利用完全平方公式即可解答.
试题解析:
982+(a-b)2=(100-2)2+a2-2ab+b2=10000-400+4+a2-2ab+b2=9604+a2-2ab+b2. (2x+y 2 )(2x-y 2 )等于( )
A. x2-y 4 B. x2-y 2 C. 4x2-y4 D. 4x2-y 2
 C
【解析】根据平方差公式可得:(2x+y 2 )(2x-y 2 )=4x2-y4 ,故选C.
C
【解析】根据平方差公式可得:(2x+y 2 )(2x-y 2 )=4x2-y4 ,故选C. 已知点M(2m -3,8),N(m -1,-3),且MN//y轴,则m=________.
 2
【解析】由MN//y轴,可得点M、N的横坐标相同,即2m-3=m-1,解得m=2.
2
【解析】由MN//y轴,可得点M、N的横坐标相同,即2m-3=m-1,解得m=2. 下列命题的逆命题不一定正确的是
A. 同位角相等,两直线平行 B. 等腰三角形的两个底角相等
C. 等腰三角形底边上的高线和中线相互重合 D. 对顶角相等
 D
【解析】选项A、B、C的逆命题都正确,选项D,对顶角相等的逆命题为相等的角为对顶角,这个命题不一定正确,例如平行四边形的对角相等,但不是对顶角,故选D.
D
【解析】选项A、B、C的逆命题都正确,选项D,对顶角相等的逆命题为相等的角为对顶角,这个命题不一定正确,例如平行四边形的对角相等,但不是对顶角,故选D. 已知分式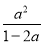 .
.
(1)当____时,分式的值等于零;
(2)当____时,分式无意义;
(3)当___且___时分式的值是正数;
(4)当____时,分式的值是负数.
 【解析】(1)根据分式值为零的条件可得a2=0,且1-2a≠0,再解即可.
(2)根据分式无意义的条件可得1-2a=0,再解方程即可;
(3)根据分式值为正可得分子分母为同号,因此1-2a>0,且a≠0,再解不等式即可;
(4)根据分式值为负可得分子分母为异号,因此1-2a<0,且a≠0,再解不等式即可.
【解析】
(1)由题意得:a2=0,且1?2a≠0,
解得:...
【解析】(1)根据分式值为零的条件可得a2=0,且1-2a≠0,再解即可.
(2)根据分式无意义的条件可得1-2a=0,再解方程即可;
(3)根据分式值为正可得分子分母为同号,因此1-2a>0,且a≠0,再解不等式即可;
(4)根据分式值为负可得分子分母为异号,因此1-2a<0,且a≠0,再解不等式即可.
【解析】
(1)由题意得:a2=0,且1?2a≠0,
解得:... 若分式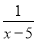 有意义,则实数
有意义,则实数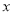 的取值范围是( )
的取值范围是( )
A. 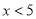 B.
B. 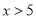 C.
C. 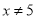 D.
D. 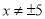
 C
【解析】根据分式的分母不等于0时,分式有意义,可列出不等式,解之即可得出答案.
【解析】
因为分式有意义,
所以,
解得,
故选C.
C
【解析】根据分式的分母不等于0时,分式有意义,可列出不等式,解之即可得出答案.
【解析】
因为分式有意义,
所以,
解得,
故选C. 分式的概念:对于式子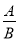 ,如果除式B中含有_____,那么称
,如果除式B中含有_____,那么称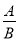 为分式,其中A称为分式的____,B称为分式的_____.
为分式,其中A称为分式的____,B称为分式的_____.
 字母 分子 分母
【解析】利用分式的概念即可得出答案.
【解析】
对于式子,如果除式B中含有字母,那么称为分式,其中A称为分式的分子,B称为分式的他、分母.
故答案为:字母;分子;分母.
字母 分子 分母
【解析】利用分式的概念即可得出答案.
【解析】
对于式子,如果除式B中含有字母,那么称为分式,其中A称为分式的分子,B称为分式的他、分母.
故答案为:字母;分子;分母.