题目内容
若分式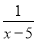 有意义,则实数
有意义,则实数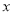 的取值范围是( )
的取值范围是( )
A. 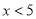 B.
B. 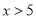 C.
C. 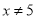 D.
D. 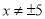
 C
【解析】根据分式的分母不等于0时,分式有意义,可列出不等式,解之即可得出答案.
【解析】
因为分式有意义,
所以,
解得,
故选C.
C
【解析】根据分式的分母不等于0时,分式有意义,可列出不等式,解之即可得出答案.
【解析】
因为分式有意义,
所以,
解得,
故选C.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(3z-y)2 等于( )
A. 9z2-y+y2 B. 9z2-yz+y2 C. 9z2-6yz+y2 D. 3z2-6yz+y2
 C
【解析】根据完全平方公式可得:(3z-y)2 =9z2-6yz+y2,故选C.
C
【解析】根据完全平方公式可得:(3z-y)2 =9z2-6yz+y2,故选C. 解下列不等式组并把解在数轴上表示出来.
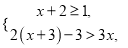
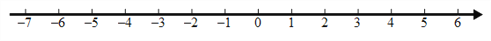
 ,在数轴上表示见解析.
【解析】试题分析:分别求出两个不等式的解集,这两个不等式解集的公共部分即为不等式组的解集,在数轴上表示出来即可.
试题解析:
由(1)得,
由(2)得,
不等式组的解集在数轴上表示如下:
,在数轴上表示见解析.
【解析】试题分析:分别求出两个不等式的解集,这两个不等式解集的公共部分即为不等式组的解集,在数轴上表示出来即可.
试题解析:
由(1)得,
由(2)得,
不等式组的解集在数轴上表示如下: 当分式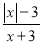 的值为0时,x的值为( )
的值为0时,x的值为( )
A. 0 B. 3 C. -3 D. ±3
 B
【解析】分式的值为0,则分子为0,分母不为0,列方程组即可求解.
【解析】
根据题意得, ,
解得,x=3;
故选B.
B
【解析】分式的值为0,则分子为0,分母不为0,列方程组即可求解.
【解析】
根据题意得, ,
解得,x=3;
故选B. 已知A、B两地相距10千米,甲从A地到B地步行需要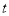 小时,乙骑自行车行同样的路程比甲少用1小时,则乙的速度可表示为__ 千米/时.
小时,乙骑自行车行同样的路程比甲少用1小时,则乙的速度可表示为__ 千米/时.
 【解析】根据“速度=路程时间”列出代数式即可.
【解析】
A、B两地之间的距离是:10千米,
乙骑自行车需要的时间是:(t?1)小时,
则乙的速度可表示为: 千米/时。
故答案是: .
【解析】根据“速度=路程时间”列出代数式即可.
【解析】
A、B两地之间的距离是:10千米,
乙骑自行车需要的时间是:(t?1)小时,
则乙的速度可表示为: 千米/时。
故答案是: . 下列式子是分式的是( )
A.  B.
B. 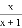 C.
C. 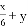 D.
D. 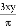
 B
【解析】A分母中不含有字母的式子是整式,故A错误;
B分母中含有字母的式子是分式,故B正确;
C分母中不含有字母的式子是整式,故C错误;
D分母中不含有字母的式子是整式,故D错误;
故选:B.
B
【解析】A分母中不含有字母的式子是整式,故A错误;
B分母中含有字母的式子是分式,故B正确;
C分母中不含有字母的式子是整式,故C错误;
D分母中不含有字母的式子是整式,故D错误;
故选:B. 分式 的值为0,则( ).
的值为0,则( ).
A.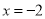 B.
B.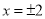 C.
C.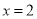 D.
D.
 C
【解析】
试题分析:根据分式的值为0的条件为分母=0,分子≠0,因此可求-4=(x+2)(x-2)=0,解得x=-2或,x=2,而x+2≠0,即x≠-2,所以x=2.
故选C
C
【解析】
试题分析:根据分式的值为0的条件为分母=0,分子≠0,因此可求-4=(x+2)(x-2)=0,解得x=-2或,x=2,而x+2≠0,即x≠-2,所以x=2.
故选C 小明解方程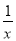 -
-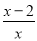 =1的过程如下:
=1的过程如下:
【解析】
方程两边乘x,得1-(x-2)=1.①
去括号,得1-x-2=1.②
移项,得-x=1-1+2.③
合并同类项,得-x=2.④
解得x=-2.⑤
所以,原分式方程的解为x=-2.⑥
请指出他解答过程中的错误,并写出正确的解答过程.
 见解析
【解析】试题分析:去分母时,注意是否每一项都乘以x,去括号,移项时,注意符合的变化;最后注意分式方程一定要检验方程的解。
【解析】
小明的解法有三处错误,步骤①去分母有误; 步骤②去括号有误;步骤⑥少检验.
正确解法为:方程两边乘x,得1-(x-2)=x.
去括号,得1-x+2=x.
移项,得-x-x=-1-2.
合并同类项,得-2x=-3.
解...
见解析
【解析】试题分析:去分母时,注意是否每一项都乘以x,去括号,移项时,注意符合的变化;最后注意分式方程一定要检验方程的解。
【解析】
小明的解法有三处错误,步骤①去分母有误; 步骤②去括号有误;步骤⑥少检验.
正确解法为:方程两边乘x,得1-(x-2)=x.
去括号,得1-x+2=x.
移项,得-x-x=-1-2.
合并同类项,得-2x=-3.
解... 

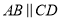 ,
, 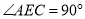 .
.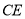 平分
平分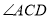 时,求证:
时,求证: 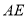 平分
平分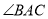 ;
;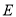 ,使
,使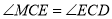 ,求证:
,求证: 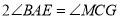 .
.