题目内容
如图，若圆心角∠AOB=110°，则圆周角∠ADB=考点：圆周角定理
专题：
分析：在优
上任取一点P，连接AP，BP，由圆周角定理求出∠P的度数，再由圆内接四边形的性质即可得出结论．
 |
| AB |
解答：
解：优
上任取一点P，连接AP，BP，
∵∠AOB=110°，
∴∠P=
∠AOB=55°．
∵四边形ADBP是圆内接四边形，
∴∠ADB=180°-∠P=180°-55°=125°．
故答案为：125°．
解：优 |
| AB |
∵∠AOB=110°，
∴∠P=
| 1 |
| 2 |
∵四边形ADBP是圆内接四边形，
∴∠ADB=180°-∠P=180°-55°=125°．
故答案为：125°．
点评：本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
相关题目
如图，单位长度为1的方格纸中，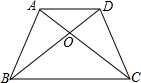
等腰梯形ABCD中，AD∥BC，AB=CD，对角线AC、BD交于点O，AC=2，∠BOC=120°，求AD+BC的值．
如图，四边形ABCD的顶点都在⊙O上，点O在四边形内部，若四边形OABC为平行四边形，则∠D等于（ ）| A、30° | B、45° |
| C、60° | D、不能确定 |
函数值y随x的增大而减小的是（ ）
| A、y=1+x | ||
B、y=
| ||
| C、y=-x+1 | ||
| D、y=-2+3x |
如图所示，四边形EFGH是四边形ABCD平移得到的．找出图中平行且相等的四条线段和一组全等的四边形．
a，b为有理数，它们表示的点在数轴上的位置如图：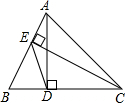
如图，在△ABC中，AD⊥BC，垂足为D，EC⊥AB，垂足为E，连接DE．试说明△BDE∽△BAC．