题目内容
1.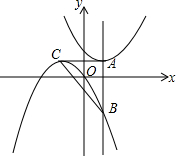 如图,在平面直角坐标系中,抛物线y=a(x-2)2+1(a为常数)的顶点为A,过点A作y轴的平行线与抛物线y=-$\frac{1}{3}$x2-$\frac{4}{3}$x交于点B.抛物线y=-$\frac{1}{3}$x2-$\frac{4}{3}$x的顶点为C,连结CA、CB,则△ABC的面积为10.
如图,在平面直角坐标系中,抛物线y=a(x-2)2+1(a为常数)的顶点为A,过点A作y轴的平行线与抛物线y=-$\frac{1}{3}$x2-$\frac{4}{3}$x交于点B.抛物线y=-$\frac{1}{3}$x2-$\frac{4}{3}$x的顶点为C,连结CA、CB,则△ABC的面积为10.
分析 由两个抛物线的解析式可以得出顶点A、C的坐标,将x=2代入y=-$\frac{1}{3}$x2-$\frac{4}{3}$x中得出B点的坐标,根据A、B、C三点的坐标即可得出AB的长以及点C到直线AB的距离h,结合三角形的面积公式即可得出结论.
解答 解:∵抛物线y=a(x-2)2+1(a为常数)的顶点为A,
∴点A的坐标为(2,1),
∵抛物线y=-$\frac{1}{3}$x2-$\frac{4}{3}$x=-$\frac{1}{3}(x+2)^{2}$+$\frac{4}{3}$,
∴点C的坐标为(-2,$\frac{4}{3}$).
令x=2,则有y=-$\frac{1}{3}$×22-$\frac{4}{3}$×2=-4,
∴点B的坐标为(2,-4),
∴AB=1-(-4)=5,点C到直线AB的距离h=2-(-2)=4,
△ABC的面积S=$\frac{1}{2}$AB•h=$\frac{1}{2}$×5×4=10.
故答案为:10.
点评 本题考查了二次函数的性质、三角形的面积公式以及点到直线的距离,解题的关键是找出A、B、C三点的坐标.本题属于基础题,难度不大,解决该题型题目时,将二次函数解析式变化成顶点式,找出点的坐标是关键.

练习册系列答案
相关题目
6.下列各式中,能用平方差公式计算的是( )
| A. | (2a+b)(a-b) | B. | (-a-b)(-a+b) | C. | (a+b)(-a-b) | D. | (-a+b)(a-b) |

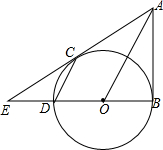 如图,过点A作⊙O的切线AB,AC,切点分别为B,C,直径BD的延长线与直线AC交于E,连接DC、OA.
如图,过点A作⊙O的切线AB,AC,切点分别为B,C,直径BD的延长线与直线AC交于E,连接DC、OA.
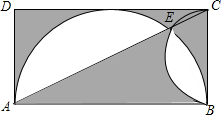 如图,长方形的长AB为8厘米,宽BC为4厘米,分别以AB、BC为直径画半圆,两个半圆的交点E在线段AC上,求阴影部分的面积.(π取3.14)
如图,长方形的长AB为8厘米,宽BC为4厘米,分别以AB、BC为直径画半圆,两个半圆的交点E在线段AC上,求阴影部分的面积.(π取3.14)