题目内容
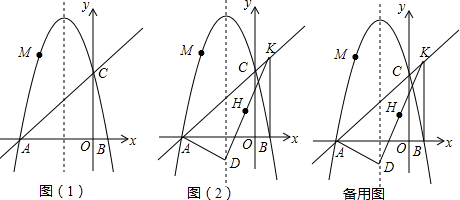
9.如图(1),已知抛物线y=ax2+bx+5与x轴交于A、B(点A在点B的左侧)两点,与y轴交于点C,已知点A的横坐标为-5,且点D(-2,-3)在此抛物线的对称轴上.(1)求a、b的值;
(2)若在直线AC上方的抛物线上存在点M,使点M到x轴的距离与M到直线AC的距离之比为$\frac{4\sqrt{2}}{3}$,试求出点M的坐标;
(3)如图(2),过点B做BK⊥x轴交直线AC于点K,连接DK、AD,点H是DK的中点,点G是线段AK上任意一点,将△DGH沿边GH翻折得△D′GH,当KG为何值时,△D′GH与△KGH重叠部分的面积是△DGK面积的$\frac{1}{4}$,请直接写出你的答案.
分析 (1)列出关于a、b的方程组解方程组即可;
(2)如图2中,作MP⊥AC于P,MG⊥AB于G,MG与AC交于点T,设点M(m,-m2-4m+5),求出MG、MP列出方程解方程即可.
(3)令y=0,得出点B和K的坐标,分三种情况:①若翻折后,点D′在直线GK上方,记D′H与GK交于点L,连接D'K,由面积的关系得出四边形D'GHK是平行四边形,再证明△ABK和△AED都是等腰直角三角形,由勾股定理得AG和KG即可;②若翻折后,点D′在直线DK下方,记D′G与KH交于点L,连接D′K,由题意得S△GHL=$\frac{1}{4}$ S△DGK=$\frac{1}{2}$ S△GHK=$\frac{1}{2}$ S△GHD′,即S△GHL=S△D′HL=S△KGL,仍证明四边形D′KGH是平行四边形,求得KG;③若翻折后,点D′于点K重合,则重叠部分的面积等于S△KGH=$\frac{1}{2}$ S△DGK,不合题意;综合写出KG的值.
解答 解:(1)∵D(-2,-3)在对称轴上,点A(-5,0)
∴抛物线的对称轴为直线x=-2,
∴$\left\{\begin{array}{l}{25a-5b+5=0}\\{-\frac{b}{2a}=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=-4}\end{array}\right.$,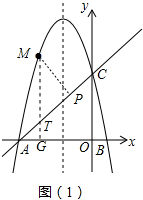
∴抛物线的解析式为y=-x2-4x+5,
∴a=-1,b=-4.
(2)如图(1)中,作MP⊥AC于P,MG⊥AB于G,MG与AC交于点T,设点M(m,-m2-4m+5),
∵AO=CO=5,∠AOC=∠AGT=∠MPT=90°,
∴∠TAG=∠ATG=∠MTP=∠PMT=45°,
∵直线AC为y=x+5,
∴点T(m,m+5),MT=-m2-4m+5-(m+5)=-m2-5m,
∴PM=$\frac{\sqrt{2}}{2}$TM=$\frac{\sqrt{2}}{2}$(-m2-5m),
∵$\frac{MG}{MP}$=$\frac{4\sqrt{2}}{3}$,
∴$\frac{-{m}^{2}-4m+5}{\frac{\sqrt{2}}{2}(-{m}^{2}-5m)}$=$\frac{4\sqrt{2}}{3}$,
解得m=-3(或-5不合题意舍弃),
∴点M坐标(-3,8).
(3)令-x2-4x+5=0,得x=-5或x=1,
∴B(1,0),K(1,6),
∵DK=$\sqrt{[1-(-2)]^{2}+[6-(-3)]^{2}}$=3$\sqrt{10}$,
①若翻折后,点D′在直线GK上方,记D′H与GK交于点L,连接D'K,如图2,
∴S△GHL=$\frac{1}{4}$S△DGK=$\frac{1}{2}$S△GHK=$\frac{1}{2}$S△GHD′,即S△GHL=S△D'GL=S△KHL,
∴GL=LK,HL=D'L,
∴四边形D'GHK是平行四边形,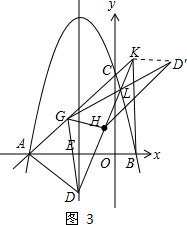
∴DG=D′G=KH=$\frac{1}{2}$KD=$\frac{3\sqrt{10}}{2}$,
又∵BK=BA=6,DE=AE=3,
∴△ABK和△AED都是等腰直角三角形,AD=3$\sqrt{2}$,
∴∠DAG=45°+45°=90°,
由勾股定理得:AG=$\sqrt{D{G}^{2}-A{D}^{2}}$=$\frac{3\sqrt{2}}{2}$,
∴KG=KA-AG=6$\sqrt{2}$-$\frac{3\sqrt{2}}{2}$=$\frac{9\sqrt{2}}{2}$,
②若翻折后,点D′在直线DK下方,记D′G与KH交于点L,连接D′K,如图3,
∴S△GHL=$\frac{1}{4}$ S△DGK=$\frac{1}{2}$ S△GHK=$\frac{1}{2}$ S△GHD′,即S△GHL=S△D′HL=S△KGL,
∴HL=KL,GL=D′L,
∴四边形D′KGH是平行四边形,
∴KG=D′H=DH=$\frac{1}{2}$ KD=$\frac{3\sqrt{10}}{2}$,
③若翻折后,点D′于点K重合,则重叠部分的面积等于S△KGH=$\frac{1}{2}$ S△DGK,不合题意;
综上所述,KG=$\frac{9\sqrt{2}}{2}$ 或KG=$\frac{3\sqrt{10}}{2}$.
点评 本题考查了用待定系数法求抛物线的解析式、用公式法求抛物线的顶点坐标、等腰三角形的判定和性质、直角三角形的判定和性质、勾股定理的运用以及全等三角形的判定和性质,题目的综合性很强.难度很大,对学生的解题能力要求较高.

| A. | 324×101 | B. | 3.24×104 | C. | 3.24×103 | D. | 32.4×102 |
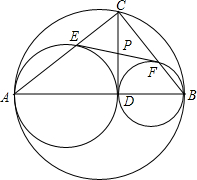 从圆上一点C向直径AB作垂线CD,D是垂足,以AD、DB为直径在大圆内分别作两个小圆,设这两个小圆的外公切线为EF,而E、F为切点,求证:CD=EF.
从圆上一点C向直径AB作垂线CD,D是垂足,以AD、DB为直径在大圆内分别作两个小圆,设这两个小圆的外公切线为EF,而E、F为切点,求证:CD=EF.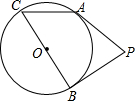 如图,点P在⊙O外,PA、PB是⊙O的切线,A、B是切点,BC是直径,若∠APB=70°,则∠ACB的度数为55°.
如图,点P在⊙O外,PA、PB是⊙O的切线,A、B是切点,BC是直径,若∠APB=70°,则∠ACB的度数为55°.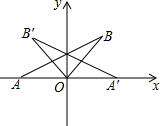 如图,在△AOB中,OA=OB,∠AOB=135°,点A的坐标为(-1,0),△AOB与△A′OB′关于y轴对称,则点B′的坐标为(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$).
如图,在△AOB中,OA=OB,∠AOB=135°,点A的坐标为(-1,0),△AOB与△A′OB′关于y轴对称,则点B′的坐标为(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$).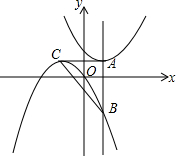 如图,在平面直角坐标系中,抛物线y=a(x-2)2+1(a为常数)的顶点为A,过点A作y轴的平行线与抛物线y=-$\frac{1}{3}$x2-$\frac{4}{3}$x交于点B.抛物线y=-$\frac{1}{3}$x2-$\frac{4}{3}$x的顶点为C,连结CA、CB,则△ABC的面积为10.
如图,在平面直角坐标系中,抛物线y=a(x-2)2+1(a为常数)的顶点为A,过点A作y轴的平行线与抛物线y=-$\frac{1}{3}$x2-$\frac{4}{3}$x交于点B.抛物线y=-$\frac{1}{3}$x2-$\frac{4}{3}$x的顶点为C,连结CA、CB,则△ABC的面积为10.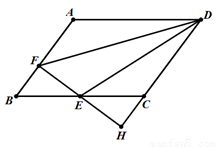
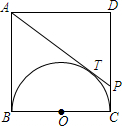 如图所示,O是正方形ABCD一边BC的中点,AP与以O为圆心,OB为半径的圆切于T点,求AT:AP的值.
如图所示,O是正方形ABCD一边BC的中点,AP与以O为圆心,OB为半径的圆切于T点,求AT:AP的值.