题目内容
5.(1)解方程:x2-6x-6=0;(2)解不等式组:$\left\{\begin{array}{l}3x-1≤2\\ 2-\frac{x+4}{2}<\frac{1-x}{3}\end{array}$.
分析 (1)利用求根公式即可直接求解;
(2)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
解答 解:(1)a=1,b=-6,c=-6,
则△=b2-4ac=36+24=60>0,
则x=$\frac{6±2\sqrt{15}}{2}$,
则x1=3+$\sqrt{15}$,x2=3-$\sqrt{15}$;
(2)$\left\{\begin{array}{l}{3x-1≤2…①}\\{2-\frac{x+4}{2}<\frac{1-x}{3}…②}\end{array}\right.$,
解①得:x≤1,
解②得:x>-2,
则不等式组的解集是:-2<x≤1.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
13.若双曲线y=$\frac{m}{x}$过点(2,6),则该双曲线一定过点( )
| A. | (-3,-4) | B. | (4,-3) | C. | (-6,2) | D. | (4,4) |
17.在四边形ABCD中,AB∥DC,AD∥BC,如果添加一个条件,即可推出该四边形是矩形,那么这个条件可以是( )
| A. | ∠D=90° | B. | OH=4 | C. | AD=BC | D. | Rt△AHB |

 如图,MN表示一段笔直的高架道路,线段AB表示高架道路旁的一排居民楼,已知点A到MN的距离为15米,BA的延长线与MN相交于点D,且∠BDN=30°,假设汽车在高速道路上行驶时,周围39米以内会受到噪音的影响.
如图,MN表示一段笔直的高架道路,线段AB表示高架道路旁的一排居民楼,已知点A到MN的距离为15米,BA的延长线与MN相交于点D,且∠BDN=30°,假设汽车在高速道路上行驶时,周围39米以内会受到噪音的影响.

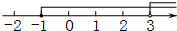

 如图,过y轴上任意一点P,作x轴的平分线,分别于反比例函数y=$\frac{4}{x}$和y=$\frac{2}{x}$的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为3.
如图,过y轴上任意一点P,作x轴的平分线,分别于反比例函数y=$\frac{4}{x}$和y=$\frac{2}{x}$的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为3.