题目内容
10. 如图,MN表示一段笔直的高架道路,线段AB表示高架道路旁的一排居民楼,已知点A到MN的距离为15米,BA的延长线与MN相交于点D,且∠BDN=30°,假设汽车在高速道路上行驶时,周围39米以内会受到噪音的影响.
如图,MN表示一段笔直的高架道路,线段AB表示高架道路旁的一排居民楼,已知点A到MN的距离为15米,BA的延长线与MN相交于点D,且∠BDN=30°,假设汽车在高速道路上行驶时,周围39米以内会受到噪音的影响.(1)过点A作MN的垂线,垂足为点H,如果汽车沿着从M到N的方向在MN上行驶,当汽车到达点P处时,噪音开始影响这一排的居民楼,那么此时汽车与点H的距离为多少米?
(2)降低噪音的一种方法是在高架道路旁安装隔音板,当汽车行驶到点Q时,它与这一排居民楼的距离QC为39米,那么对于这一排居民楼,高架道路旁安装的隔音板至少需要多少米长?(精确到1米)(参考数据:$\sqrt{3}$≈1.7)
分析 (1)连接PA.在直角△PAH中利用勾股定理来求PH的长度;
(2)由题意知,隔音板的长度是PQ的长度.通过解Rt△ADH、Rt△CDQ分别求得DH、DQ的长度,然后结合图形得到:PQ=PH+DQ-DH,把相关线段的长度代入求值即可.
解答 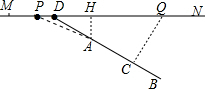 解:(1)如图,连接PA.由题意知,AP=39m.在直角△APH中,PH=$\sqrt{A{P}^{2}-A{H}^{2}}$=$\sqrt{3{9}^{2}-1{5}^{2}}$=36(米);
解:(1)如图,连接PA.由题意知,AP=39m.在直角△APH中,PH=$\sqrt{A{P}^{2}-A{H}^{2}}$=$\sqrt{3{9}^{2}-1{5}^{2}}$=36(米);
(2)由题意知,隔音板的长度是PQ的长度.
在Rt△ADH中,DH=AH•cot30°=15$\sqrt{3}$(米).
在Rt△CDQ中,DQ=$\frac{CQ}{sin30°}$=$\frac{39}{\frac{1}{2}}$=78(米).
则PQ=PH+HQ=PH+DQ-DH=36+78-15$\sqrt{3}$≈114-15×1.7=88.5≈89(米).
答:高架道路旁安装的隔音板至少需要89米.
点评 本题考查了解直角三角形的应用、勾股定理的应用.根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.

练习册系列答案
相关题目
18. 据报道,历经一百天的调查研究,南京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车每行驶20千米平均向大气里排放0.035千克污染物.校环保志愿小分队从环保局了解到南京100天的空气质量等级情况,并制成统计图和表:
据报道,历经一百天的调查研究,南京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车每行驶20千米平均向大气里排放0.035千克污染物.校环保志愿小分队从环保局了解到南京100天的空气质量等级情况,并制成统计图和表:
2014年南京市100天空气质量等级天数统计表
(1)表中a=25,b=20,图中严重污染部分对应的圆心角n=72°.
(2)请你根据“2014年南京市100天空气质量等级天数统计表”计算100天内重度污染和严重污染出现的频率共是多少?
(3)小明是社区环保志愿者,他和同学们调查了机动车每天的行驶路程,了解到每辆车每天平均出行25千米.已知南京市2014年机动车保有量已突破200万辆,请你通过计算,估计2014年南京市一天中出行的机动车至少要向大气里排放多少千克污染物?
 据报道,历经一百天的调查研究,南京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车每行驶20千米平均向大气里排放0.035千克污染物.校环保志愿小分队从环保局了解到南京100天的空气质量等级情况,并制成统计图和表:
据报道,历经一百天的调查研究,南京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车每行驶20千米平均向大气里排放0.035千克污染物.校环保志愿小分队从环保局了解到南京100天的空气质量等级情况,并制成统计图和表:2014年南京市100天空气质量等级天数统计表
| 空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 天数(天) | 10 | a | 12 | 8 | 25 | b |
(2)请你根据“2014年南京市100天空气质量等级天数统计表”计算100天内重度污染和严重污染出现的频率共是多少?
(3)小明是社区环保志愿者,他和同学们调查了机动车每天的行驶路程,了解到每辆车每天平均出行25千米.已知南京市2014年机动车保有量已突破200万辆,请你通过计算,估计2014年南京市一天中出行的机动车至少要向大气里排放多少千克污染物?
15.正八边形的内角和等于( )
| A. | 720° | B. | 1080° | C. | 1440° | D. | 1880° |
2. 如图,数轴上有A,B,C,D四个点,其中表示互为倒数的点是( )
如图,数轴上有A,B,C,D四个点,其中表示互为倒数的点是( )
 如图,数轴上有A,B,C,D四个点,其中表示互为倒数的点是( )
如图,数轴上有A,B,C,D四个点,其中表示互为倒数的点是( )| A. | 点A与点B | B. | 点A与点D | C. | 点B与点D | D. | 点B与点C |
20.将二次函数y=x2的图象向右平移3个单位,再向上平移7个单位后,所得图象的函数表达式是( )
| A. | y=(x-3)2+7 | B. | y=(x+3)2+7 | C. | y=(x-3)2-7 | D. | y=(x+3)2-7 |
 如图,将矩形ABCD绕点A顺时针旋转到AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=120°,则∠α=30°.
如图,将矩形ABCD绕点A顺时针旋转到AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=120°,则∠α=30°. 如图,已知在△ABC中,AB=AC,以AB为直径的⊙O与边BC交于点E,与边AC交于点F,过点E作ED⊥AC于D.
如图,已知在△ABC中,AB=AC,以AB为直径的⊙O与边BC交于点E,与边AC交于点F,过点E作ED⊥AC于D.