题目内容
如图，若l1∥l2，∠1=45°，则∠2=_____.
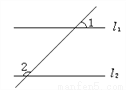
135
【解析】试题分析：根据对顶角的性质求出∠1的对顶角，然后根据两直线平行同旁内角互补得出∠2的度数.
阳光试卷单元测试卷系列答案下列说法中:
①P是线段AB上的一点,直线l经过点P且l⊥AB,则l是线段AB的垂直平分线;
②直线l经过线段AB的中点,则l是线段AB的垂直平分线;
③若AP=PB,且直线l垂直于线段AB,则l是线段AB的垂直平分线;
④经过线段AB的中点P且垂直于AB的直线l是线段AB的垂直平分线.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
A
【解析】根据线段的垂直平分线的定义，以及定理：到线段的两端距离相等的点在线段的垂直平分线上，即可判断．
【解析】
①当P不是AB的中点，则直线l不平分线段AB，故错误；
②直线l经过线段AB的中点，且垂直于AB则l是线段AB的垂直平分线，故错误；
③若AP=PB，则P在线段AB的垂直平分线上，但l不一定过点P，所以直线l不一定是线段AB的垂直平分线，故错误；
④... 在△ABC中，若|sinA－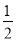
|＋(
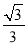－tanB)2＝0，则∠C的度数为( )
A. 30° B. 60° C. 90° D. 120°
D
【解析】试题解析：∵|sinA-|+（-tanB）2=0，
∴|sinA-|=0，（ -tanB）2=0，
∴sinA-=0， -tanB=0，
sinA=，tanB=
∴∠A=30°，∠B=30°，
∴∠C=120°．
故选D． 下列命题正确的是（ ）
A．内错角相等
B．相等的角是对顶角
C．三条直线相交 ，必产生同位角、内错角、同旁内角
D．同位角相等，两直线平行
D．
【解析】
试题分析：A．只有两直线平行，内错角才相等，故错误；
B．对顶角相等，但相等的角不一定是对顶角，故错误；
C．必须出现“三线八角”的形式，即两直线被第三条直线所截，才产生同位角，内错角，同旁内角，故错误；
D．平行线的判定定理，故正确．
故选D． 如图，AD∥BC，AC与BD相交于O，则图中相等的角有_____对.
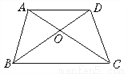
四
【解析】∵∠AOB与∠COD是对顶角，∠AOD与∠BOC是对顶角，
∴∠AOB=∠COD，∠AOD=∠BOC.
∵AD∥BC,
∴∠CAD=∠ACB，∠ADB=∠CBD.
∴图中相等的角有四对. 如图，l是线段AB的对称轴，l′是线段BC的对称轴，l和l′相交于点O．OA与OC相等吗？为什么？
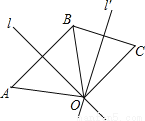
相等，理由见解析
【解析】试题分析：由轴对称的性质即可证明．
试题解析：【解析】
∵l是线段AB的对称轴，∴OA=OB，
∵l′是线段BC的对称轴，∴OB=OC，
∴OA=OC． 下列语句中，正确的个数有（ ）
①两个关于某直线对称的图形是全等的
②两个图形关于某直线对称，对称点一定在该直线的两旁
③两个成轴对称的图形的对应点连线的垂直平分线，就是它们的对称轴
④平面内两个全等的图形一定关于某直线对称．
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】【解析】
①两个关于某直线对称的图形是全等的，此选项正确；
②两个图形关于某直线对称，对称点一定在该直线的两旁也有可能在直线上，此选项错误；
③两个成轴对称的图形的对应点连线的垂直平分线，就是它们的对称轴，此选项正确；
④平面内两个全等的图形不一定关于某直线对称，故此选项错误．
故选B． 若(3x+1)-3有意义,则x的取值范围是___________.
x≠-
【解析】(3x+1)-3= ，根据分式有意义的条件可得3x+1≠0，即. 已知：如图，AB∥CD，EF分别交于AB、CD于E、F，EG平分∠AEF，FH平分∠EFD。
求证： EG∥FH
证明：∵ AB∥CD（已知），∴ ∠AEF=∠EFD （______）。∵ EG平分∠AEF，FH平分∠EFD（______），∴∠______=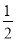
∠AEF，∠______=
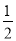∠EFD（角平分线定义）。∴ ∠______=∠______，∴ EG∥FH（______）。
两直线平行，内错角相等，已知，∠GEF，∠EFH，∠GEF，∠EFH，内错角相等，两直线平行。
【解析】试题分析：本题只要根据平行线的性质以及角平分线的性质得出角相等，最后根据内错角相等，两直线平行得出答案．