题目内容
20.已知直角梯形ABCD中,AD∥BC,∠B=90°,AB=4,AD=2,CD=5,那么BC=5.分析 过点D作DE⊥BC于点E,易证四边形ABED是矩形,所以可得AD=BE,AB=DE,在直角三角形DEC中,利用勾股定理可求出CE的长,进而可求出BC的长.
解答 解:过点D作DE⊥BC于点E,
∵AD∥BC,∠B=90°,
∴四边形ABED是矩形,
∴AD=BE=2,AB=DE=4,
在直角三角形DEC中,CD=5,
∴CE=$\sqrt{C{D}^{2}-D{E}^{2}}$=3,
∴BC=BE+CE=2+3=5,
故答案为:5.
点评 本题考查了直角梯形的性质以及勾股定理的运用,正确做出图形的辅助线构造直角三角形是解题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
8. 如图所示,若干个全等的正五边形排成环状,要完成这一圆环共需要正五边形的个数为( )
如图所示,若干个全等的正五边形排成环状,要完成这一圆环共需要正五边形的个数为( )
 如图所示,若干个全等的正五边形排成环状,要完成这一圆环共需要正五边形的个数为( )
如图所示,若干个全等的正五边形排成环状,要完成这一圆环共需要正五边形的个数为( )| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
 已知:如图,在?ABCD中,AB=2cm,AD=5cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=3cm.
已知:如图,在?ABCD中,AB=2cm,AD=5cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=3cm. 一副三角板按如图(4)所示叠放在一起,若固定△AOB,将△ACD绕着公共顶点A,按顺时针方向旋转α度(0°<α<180°),当△ACD的边CD与△AOB的某一边平行时,相应的旋转角α的值是30°,75°,165°.
一副三角板按如图(4)所示叠放在一起,若固定△AOB,将△ACD绕着公共顶点A,按顺时针方向旋转α度(0°<α<180°),当△ACD的边CD与△AOB的某一边平行时,相应的旋转角α的值是30°,75°,165°.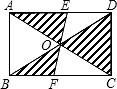 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=4cm,BC=6cm,则图中阴影部分的面积为12cm2.
如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=4cm,BC=6cm,则图中阴影部分的面积为12cm2.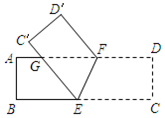 如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E交AF于点G,若∠CEF=80°,则∠GFD′=20°.
如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E交AF于点G,若∠CEF=80°,则∠GFD′=20°.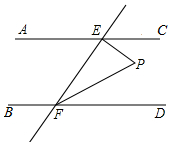 如图,若AC∥BD,EF与AC、BD分别相交于E、F,∠EFD的平分线FP与EP相交于点P.
如图,若AC∥BD,EF与AC、BD分别相交于E、F,∠EFD的平分线FP与EP相交于点P.