题目内容
12.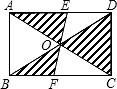 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=4cm,BC=6cm,则图中阴影部分的面积为12cm2.
如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=4cm,BC=6cm,则图中阴影部分的面积为12cm2.
分析 首先结合矩形的性质证明△AOE≌△COF,得△AOE、△COF的面积相等,从而将阴影部分的面积转化为△BCD的面积.
解答 解:∵四边形ABCD是矩形,
∴OA=OC,∠AEO=∠CFO;
又∵∠AOE=∠COF,
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠AEO=∠CFO}\\{OA=OC}\\{∠AOE=∠COF}\end{array}\right.$,
∴△AOE≌△COF,得S△AOE=S△COF,
∴S阴影=S△AOE+S△BOF+S△COD=S△AOE+S△BOF+S△COD=S△BCD;
∵S△BCD=$\frac{1}{2}$BC•CD=12,故S阴影=12.
故答案为12.
点评 此题主要考查了矩形的性质以及全等三角形的判定和性质,能够根据三角形全等,从而将阴影部分的面积转化为矩形面积的一半,是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在平行四边形ABCD中,∠A的平分线交BC于点F,若AB=10 cm,AD=16 cm,则FC=6cm.
如图,在平行四边形ABCD中,∠A的平分线交BC于点F,若AB=10 cm,AD=16 cm,则FC=6cm.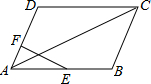 如图,在?ABCD中,E是边AB的中点,F是边AD上一点,AF=$\frac{1}{2}$FD,连结EF交AC于点G,若AC=10,则AG的长为2.
如图,在?ABCD中,E是边AB的中点,F是边AD上一点,AF=$\frac{1}{2}$FD,连结EF交AC于点G,若AC=10,则AG的长为2.