题目内容
10. 如图,在平面直角坐标系中,四边形OABC是边长为8的正方形,M(8,m)、N(n,8)分别是线段AB、BC上的两个动点,且ON⊥MN,当OM最小时,m+n=10.
如图,在平面直角坐标系中,四边形OABC是边长为8的正方形,M(8,m)、N(n,8)分别是线段AB、BC上的两个动点,且ON⊥MN,当OM最小时,m+n=10.
分析 易证得△OCN∽NBM,则$\frac{CN}{BM}=\frac{OC}{NB}$,由此可求得m与n的关系式,从而得到t的取值范围.由勾股定理可得ON=$\sqrt{O{A}^{2}+A{M}^{2}}$=$\sqrt{64+{m}^{2}}$,结合m的取值范围可得ON的最小值,从而求得m、n的值.
解答 解:由题意可得OC=OA=8,CN=n,BN=8-n,AM=m,BM=8-m
∵四边形OABC是正方形,
∴∠C=∠B=90°,
∵ON⊥MN,
∴∠MNO=90°,
∵∠ONC+∠CON=90°,∠ONC+∠BNM=90°,
∴∠CON=∠BNM,
∴△OCN∽NBM,
∴$\frac{CN}{BM}=\frac{OC}{NB}$,
即$\frac{n}{8-m}=\frac{8}{8-n}$,整理得(n-4)2=8m-48,
∵(n-4)2≥0,
∴8m-48≥0,
∴m≥6.
∵OM=$\sqrt{O{A}^{2}+A{M}^{2}}$=$\sqrt{64+{m}^{2}}$,
∴当m=6时,OM取得最小值,最小值为10.此时n=4.
∴当当OM最小时,m+n=10.
故答案为:10.
点评 本题考查了正方形的性质,相似三角形的判断,判断出m的取值范围是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
5. 如图,Rt△ACB中,AC=BC,∠ACB=90°,D、E为AB上两点,且∠DCE=45°,F为△ABC外一点,且FB⊥AB,FC⊥CD,则下列结论:
如图,Rt△ACB中,AC=BC,∠ACB=90°,D、E为AB上两点,且∠DCE=45°,F为△ABC外一点,且FB⊥AB,FC⊥CD,则下列结论:
①CD=CF;②CE垂直但不平分DF;③AD2+BD2=2DC2;④DE2-BE2=AD2.
其中正确的个数是( )
 如图,Rt△ACB中,AC=BC,∠ACB=90°,D、E为AB上两点,且∠DCE=45°,F为△ABC外一点,且FB⊥AB,FC⊥CD,则下列结论:
如图,Rt△ACB中,AC=BC,∠ACB=90°,D、E为AB上两点,且∠DCE=45°,F为△ABC外一点,且FB⊥AB,FC⊥CD,则下列结论:①CD=CF;②CE垂直但不平分DF;③AD2+BD2=2DC2;④DE2-BE2=AD2.
其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,…按照这种移动规律进行下去,第51次移动到点A51,那么点A51所表示的数为( )
如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,…按照这种移动规律进行下去,第51次移动到点A51,那么点A51所表示的数为( )
 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,…按照这种移动规律进行下去,第51次移动到点A51,那么点A51所表示的数为( )
如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,…按照这种移动规律进行下去,第51次移动到点A51,那么点A51所表示的数为( )| A. | -74 | B. | -77 | C. | -80 | D. | -83 |
20.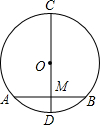 如图,⊙O中,直径CD=10cm,弦AB⊥CD于点M,OM:MD=3:2,则AB的长是( )
如图,⊙O中,直径CD=10cm,弦AB⊥CD于点M,OM:MD=3:2,则AB的长是( )
 如图,⊙O中,直径CD=10cm,弦AB⊥CD于点M,OM:MD=3:2,则AB的长是( )
如图,⊙O中,直径CD=10cm,弦AB⊥CD于点M,OM:MD=3:2,则AB的长是( )| A. | 4cm | B. | 5cm | C. | 6cm | D. | 8cm |
 如图,在⊙O中,P为$\widehat{BAC}$的中点,PD⊥CD,CD交⊙O于A,若AC=3,AD=2,则AB的长为7.
如图,在⊙O中,P为$\widehat{BAC}$的中点,PD⊥CD,CD交⊙O于A,若AC=3,AD=2,则AB的长为7.
 如图,M、P分别为△ABC的AB、AC上的点,且AM=BM,AP=2CP,BP与CM相交于N,已知PN=1,则PB的长为( )
如图,M、P分别为△ABC的AB、AC上的点,且AM=BM,AP=2CP,BP与CM相交于N,已知PN=1,则PB的长为( )