题目内容
13.化简:(1)$\frac{1}{3}$$\sqrt{{x}^{2}y}$•(-4$\sqrt{\frac{{y}^{2}}{x}}$)$÷\frac{1}{6}$$\sqrt{{x}^{2}y}$;
(2)$\sqrt{3}$$÷\sqrt{2}$×$\frac{14}{\sqrt{3}-\sqrt{2}}$-($\sqrt{24}$$+\sqrt{12}$)
分析 (1)根据二次根式的乘除法则运算;
(2)先把各二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.
解答 解:(1)原式=$\frac{1}{3}$•(-4)•6•$\sqrt{{x}^{2}y•\frac{{y}^{2}}{x}•\frac{1}{{x}^{2}y}}$
=-$\frac{-8y\sqrt{x}}{x}$;
(2)原式=$\sqrt{3}$×$\frac{\sqrt{2}}{2}$×14($\sqrt{3}$+$\sqrt{2}$)-2$\sqrt{6}$-2$\sqrt{3}$
=21$\sqrt{2}$+14$\sqrt{3}$-2$\sqrt{6}$-2$\sqrt{3}$
=21$\sqrt{2}$+12$\sqrt{3}$-2$\sqrt{6}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
2.若长方形的一边长为3m+n,另一边比它长m-n(m>n),则这个长方形的面积是( )
| A. | 12m2+4mn | B. | 12m2-4mn | C. | 3m2-2mn-n2 | D. | 3m2+2mn-n2 |
 如图,在四边形ABCD中,AO是∠DAB的平分线,BO是∠ABC的平分线,AO与BO交于点O.若∠C+∠D=120°,求∠AOB的度数.
如图,在四边形ABCD中,AO是∠DAB的平分线,BO是∠ABC的平分线,AO与BO交于点O.若∠C+∠D=120°,求∠AOB的度数.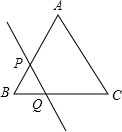 如图,在正△ABC中,AB=10cm,直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/s,运动时间为t(s)(0<t<5),则BP=$\frac{2\sqrt{3}}{3}t$.(用t的代数式表示)
如图,在正△ABC中,AB=10cm,直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/s,运动时间为t(s)(0<t<5),则BP=$\frac{2\sqrt{3}}{3}t$.(用t的代数式表示) 如图,在平面直角坐标系中,四边形OABC是边长为8的正方形,M(8,m)、N(n,8)分别是线段AB、BC上的两个动点,且ON⊥MN,当OM最小时,m+n=10.
如图,在平面直角坐标系中,四边形OABC是边长为8的正方形,M(8,m)、N(n,8)分别是线段AB、BC上的两个动点,且ON⊥MN,当OM最小时,m+n=10.