题目内容
9.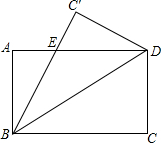 如图,把矩形纸片沿对角线BD折叠,设重叠部分为△EBD,则下列结论中错误的是( )
如图,把矩形纸片沿对角线BD折叠,设重叠部分为△EBD,则下列结论中错误的是( )| A. | ∠ABE=∠C′DE | B. | EB=ED | C. | EA=EC′ | D. | ∠ABE等于30° |
分析 根据四边形ABCD为矩形,可得∠BAE=∠DC′E,AB=C′D,再由对顶角相等可得∠AEB=∠C′ED,所以△AEB≌△C′ED,就可以得出BE=DE,由此判断即可.
解答 解:∵四边形ABCD为矩形
∴∠BAE=∠DC′E,AB=C′D,故A、B选项正确;
在△AEB和△C′ED中,
$\left\{\begin{array}{l}{∠BAE=∠DC′E}\\{∠AEB=∠C′ED}\\{AB=C′D}\end{array}\right.$,
∴△AEB≌△C′ED(AAS),
∴∠ABE=∠C′DE,BE=DE,EA=EC′,故ABC正确;
∵得不出∠ABE=∠EBD,
∴∠ABE不一定等于30°,故D错误.
故选:D.
点评 本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变.

练习册系列答案
相关题目
19.近期由于雾霾严重,不少市民选择佩戴口罩出行,某药店购进甲种可预防PM2.5的N95型口罩和乙种普通口罩共400个,这两种口罩的进价和售价如表所示:
该药店计划购进乙种口罩x个,两种口罩全部销售完后可获毛利润y元.
注:毛利润=(售价-进价)×销售量
(1)求出毛利润y与x的函数关系式;
(2)已知甲种口罩的数量不多于乙种口罩数量的3倍,该药店怎样进货,使全部销售获得的毛利润最大?并求出最大毛利润.
| 甲 | 乙 | |
| 进价(元/个) | 18 | 6 |
| 售价(元/个) | 22 | 9 |
注:毛利润=(售价-进价)×销售量
(1)求出毛利润y与x的函数关系式;
(2)已知甲种口罩的数量不多于乙种口罩数量的3倍,该药店怎样进货,使全部销售获得的毛利润最大?并求出最大毛利润.
4.下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有9个,第(2)个图形中面积为1的正方形有14个,…,按此规律.则第(10)个图形中面积为1的正方形的个数为( )


| A. | 72 | B. | 64 | C. | 54 | D. | 50 |
14.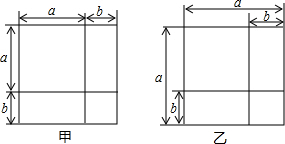 利用图形中面积的等量关系可以得到某些数学公式,例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )
利用图形中面积的等量关系可以得到某些数学公式,例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )
 利用图形中面积的等量关系可以得到某些数学公式,例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )
利用图形中面积的等量关系可以得到某些数学公式,例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )| A. | a2-b2=(a-b)2 | B. | (a+b)2=a2+2ab+b2 | C. | (a-b)2=a2-2ab+b2 | D. | a2-b2=(a+b)(a-b) |
1.下列运算正确的是( )
| A. | x2+x3=x5 | B. | (x4)2=x6 | C. | x6÷x2=x3 | D. | (-x5)4=x20 |
 ).
).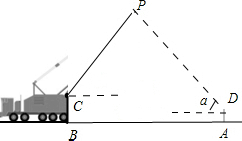 如图,是一辆吊车的示意图,小明站在距吊车底部点B为10米的A处看到吊车的起重臂顶端P处的仰角a为45°,已知吊车的起重臂底端C处与地面的距离(线段BC的长)为3.2米,起重臂CP与水平方向的夹角β为53.1°,小明的眼睛D处距地面为1.6米,求吊车的起重臂CP的长度和点P到地面的距离.(参考数据:sin53.1°≈0.8,cos53.1°≈0.6,tan53.1°≈$\frac{3}{4}$)
如图,是一辆吊车的示意图,小明站在距吊车底部点B为10米的A处看到吊车的起重臂顶端P处的仰角a为45°,已知吊车的起重臂底端C处与地面的距离(线段BC的长)为3.2米,起重臂CP与水平方向的夹角β为53.1°,小明的眼睛D处距地面为1.6米,求吊车的起重臂CP的长度和点P到地面的距离.(参考数据:sin53.1°≈0.8,cos53.1°≈0.6,tan53.1°≈$\frac{3}{4}$)