题目内容
20.超市按标价销售某种商品时,每件获利45元,按标价八五折销售该商品8件与将标价降低35元销售12件所获利润相同.(1)该商品每件进价,标价分别是多少?
(2)若每件按标价售出,超市每天可售该商品100件,若每件降价1元,则超市每天多售该商品4件.问每件商品降价多少元出售,每天获利最大?最大利润是多少元?
分析 (1)设每件商品标价x元,则根据题意列出方程8[0.85x-(x-45)]=12(45-35),求出方程的解即可;
(2)设每件商品降价x元,每天获利y元,根据题意列出解析式y=(45-x)(100+4x),求出函数的最值即可.
解答 解:(1)设每件商品标价x元,则根据题意得:
8[0.85x-(x-45)]=12(45-35),
解得:x=200,
x-45=155,
答:该商品每件进价155元,标件每件200元;
(2)设每件商品降价x元,每天获利y元,则
y=(45-x)(100+4x)
=-4(x+25)(x-45),
∵-4<0,
∴当x=$\frac{-25+45}{2}$=10时,y最大=4900,
答:每件商品降价10元时,每天获利最大为4900元.
点评 本题考查了二次函数的最值,一元一次方程的应用,解此题的关键是能根据题意列出方程和二次函数的解析式,题目比较典型,有一定的难度.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
11.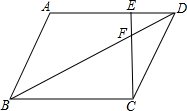 如图,在?ABCD中,点E在AD上,EC交对角线BD于点F,AE:ED=2:1,则EF:FC等于( )
如图,在?ABCD中,点E在AD上,EC交对角线BD于点F,AE:ED=2:1,则EF:FC等于( )
 如图,在?ABCD中,点E在AD上,EC交对角线BD于点F,AE:ED=2:1,则EF:FC等于( )
如图,在?ABCD中,点E在AD上,EC交对角线BD于点F,AE:ED=2:1,则EF:FC等于( )| A. | 1:1 | B. | 1:2 | C. | 1:3 | D. | 2:3 |
15.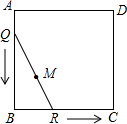 如图,正方形ABCD的边长为1,将长为1的线段QR的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,按A→B→C→D→A的方向滑动到A停止,同时点R从点B出发,按B→C→D→A→B的方向滑动到B停止,在这个过程中,线段QR的中点M所经过的路线围成的图形面积为( )
如图,正方形ABCD的边长为1,将长为1的线段QR的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,按A→B→C→D→A的方向滑动到A停止,同时点R从点B出发,按B→C→D→A→B的方向滑动到B停止,在这个过程中,线段QR的中点M所经过的路线围成的图形面积为( )
 如图,正方形ABCD的边长为1,将长为1的线段QR的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,按A→B→C→D→A的方向滑动到A停止,同时点R从点B出发,按B→C→D→A→B的方向滑动到B停止,在这个过程中,线段QR的中点M所经过的路线围成的图形面积为( )
如图,正方形ABCD的边长为1,将长为1的线段QR的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,按A→B→C→D→A的方向滑动到A停止,同时点R从点B出发,按B→C→D→A→B的方向滑动到B停止,在这个过程中,线段QR的中点M所经过的路线围成的图形面积为( )| A. | $\frac{π}{4}$ | B. | 4-π | C. | π | D. | $\frac{4-π}{4}$ |
5. 如图,将长为2,宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n可能是( )
如图,将长为2,宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n可能是( )
 如图,将长为2,宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n可能是( )
如图,将长为2,宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n可能是( )| A. | 2或4 | B. | 2或3 | C. | 3或5 | D. | 2或5 |
9.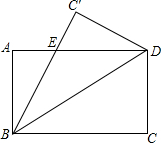 如图,把矩形纸片沿对角线BD折叠,设重叠部分为△EBD,则下列结论中错误的是( )
如图,把矩形纸片沿对角线BD折叠,设重叠部分为△EBD,则下列结论中错误的是( )
 如图,把矩形纸片沿对角线BD折叠,设重叠部分为△EBD,则下列结论中错误的是( )
如图,把矩形纸片沿对角线BD折叠,设重叠部分为△EBD,则下列结论中错误的是( )| A. | ∠ABE=∠C′DE | B. | EB=ED | C. | EA=EC′ | D. | ∠ABE等于30° |
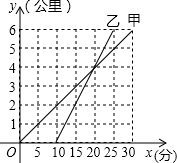 甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图.请你根据图象解决下列问题:
甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图.请你根据图象解决下列问题: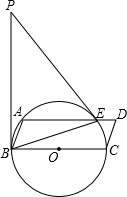 如图,BC为⊙O的直径,点A为⊙O上的点,以BC、AB为边作?ABCD,⊙O交于AD与点E,连接BE,点P是过点B的⊙O的切线上的一点.连结PE,且满足∠PEA=∠ABE.
如图,BC为⊙O的直径,点A为⊙O上的点,以BC、AB为边作?ABCD,⊙O交于AD与点E,连接BE,点P是过点B的⊙O的切线上的一点.连结PE,且满足∠PEA=∠ABE.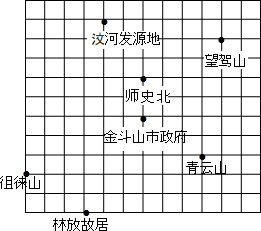 图中是某市旅游景点示意图,请建立适当的坐标系,使横轴与网格线的横线平行,纵轴与网格线的竖线平行,并且使青云山的坐标为(3,-2),然后再写出下列各景点的坐标.
图中是某市旅游景点示意图,请建立适当的坐标系,使横轴与网格线的横线平行,纵轴与网格线的竖线平行,并且使青云山的坐标为(3,-2),然后再写出下列各景点的坐标.