题目内容
17.请写出一个开口向下,与y轴交点的纵坐标为3的抛物线的函数表达式y=-x2+x+3( ).
).
分析 首先根据开口向下得到二次项系数小于0,然后根据与y轴的交点坐标的纵坐标为3得到c值即可得到函数的解析式.
解答 解:∵开口向下,
∴y=ax2+bx+c中a<0,
∵与y轴的交点纵坐标为3,
∴c=3,
∴抛物线的解析式可以为:y=-x2+x+3(答案不唯一).
故答案为:y=-x2+x+3(答案不唯一).
点评 本题考查了二次函数的性质,解题的关键是熟知二次函数中各项系数的作用.

练习册系列答案
相关题目
5. 如图,将长为2,宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n可能是( )
如图,将长为2,宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n可能是( )
 如图,将长为2,宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n可能是( )
如图,将长为2,宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n可能是( )| A. | 2或4 | B. | 2或3 | C. | 3或5 | D. | 2或5 |
9.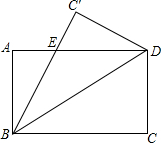 如图,把矩形纸片沿对角线BD折叠,设重叠部分为△EBD,则下列结论中错误的是( )
如图,把矩形纸片沿对角线BD折叠,设重叠部分为△EBD,则下列结论中错误的是( )
 如图,把矩形纸片沿对角线BD折叠,设重叠部分为△EBD,则下列结论中错误的是( )
如图,把矩形纸片沿对角线BD折叠,设重叠部分为△EBD,则下列结论中错误的是( )| A. | ∠ABE=∠C′DE | B. | EB=ED | C. | EA=EC′ | D. | ∠ABE等于30° |
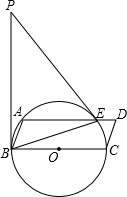 如图,BC为⊙O的直径,点A为⊙O上的点,以BC、AB为边作?ABCD,⊙O交于AD与点E,连接BE,点P是过点B的⊙O的切线上的一点.连结PE,且满足∠PEA=∠ABE.
如图,BC为⊙O的直径,点A为⊙O上的点,以BC、AB为边作?ABCD,⊙O交于AD与点E,连接BE,点P是过点B的⊙O的切线上的一点.连结PE,且满足∠PEA=∠ABE.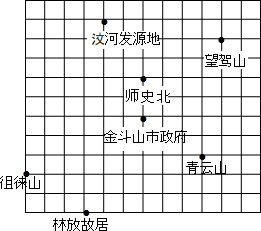 图中是某市旅游景点示意图,请建立适当的坐标系,使横轴与网格线的横线平行,纵轴与网格线的竖线平行,并且使青云山的坐标为(3,-2),然后再写出下列各景点的坐标.
图中是某市旅游景点示意图,请建立适当的坐标系,使横轴与网格线的横线平行,纵轴与网格线的竖线平行,并且使青云山的坐标为(3,-2),然后再写出下列各景点的坐标.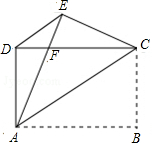 如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.