题目内容
11.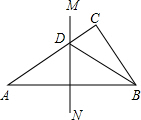 如图,在△ABC中,∠C=90°,AC=1cm,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD,若CD:DB=3:5,求CD的长和△ABC的面积.
如图,在△ABC中,∠C=90°,AC=1cm,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD,若CD:DB=3:5,求CD的长和△ABC的面积.
分析 由于CD:DB=3:5,可设DC=3x,BD=5x,由于MN是线段AB的垂直平分线,故AD=DB,AD=5x,又知AC=16cm,即可据此列方程解答.
解答 解:∵CD:DB=3:5,
∴设DC=3x,BD=5x,
又∵MN是线段AB的垂直平分线,
∴AD=DB=5x,
又∵AC=16cm,
∴3x+5x=16,
解得:x=2,
∴CD=6cm,DB=10cm,
在Rt△BDC中,CD=6cm,DB=10cm,
在Rt△BDC中,CD=6cm,DB=10cm,
∴BC=$\sqrt{D{B}^{2}-C{D}^{2}}$=8cm,
∴△ABC的面积=$\frac{1}{2}$AC×BC=$\frac{1}{2}$×16×8=64(cm2).
答:CD的长为6cm,△ABC的面积为64cm2.
点评 本题考查了线段垂直平分线的性质、勾股定理、解直角三角形的相关知识,综合性较强,计算要仔细.

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
3.平行四边形、矩形、菱形、正方形都具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | C. | 对角线相等 | D. | 轴对称图形 |
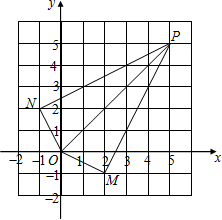 在如图中的网格中建立平面直角坐标系,在坐标平面内描出点O(0,0),P(5,5),M(2,-1),N(-1,2),连接OP,OM,ON,PM,PN,并直接回答下列问题:
在如图中的网格中建立平面直角坐标系,在坐标平面内描出点O(0,0),P(5,5),M(2,-1),N(-1,2),连接OP,OM,ON,PM,PN,并直接回答下列问题: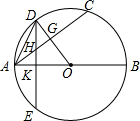 如图,AB是⊙O的直径,AC为⊙O的弦,半径0D⊥AC于G.弦DE⊥AB于K,交AC于H.
如图,AB是⊙O的直径,AC为⊙O的弦,半径0D⊥AC于G.弦DE⊥AB于K,交AC于H.