题目内容
1.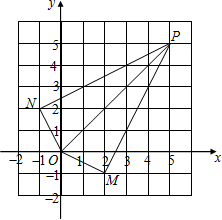 在如图中的网格中建立平面直角坐标系,在坐标平面内描出点O(0,0),P(5,5),M(2,-1),N(-1,2),连接OP,OM,ON,PM,PN,并直接回答下列问题:
在如图中的网格中建立平面直角坐标系,在坐标平面内描出点O(0,0),P(5,5),M(2,-1),N(-1,2),连接OP,OM,ON,PM,PN,并直接回答下列问题:(1)判断△OPN与△MOP的形状,并说明理由;
(2)求证:OP平分∠NPM.
分析 (1)利用勾股定理的逆定理求出△PNO是直角三角形,同理可得出△PMO是直角三角形,即可得出答案;
(2)利用角平分线的性质进行证明.
解答 (1)解:△OPN与△MOP都是直角三角形,理由如下:
∵NO=$\sqrt{5}$,MO=$\sqrt{5}$,NP=3$\sqrt{5}$,PM=3$\sqrt{5}$,OP=5$\sqrt{2}$,
∴NO2+NP2=OP2,
∴△PNO是直角三角形,
同理可得出△PMO是直角三角形;
(2)证明:由(1)知,△PNO是直角三角形,△PMO是直角三角形,则OM⊥PM,ON⊥PN.
又∵OM=ON=$\sqrt{5}$,
∴OP是∠NPM的平分线,即OP平分∠NPM.
点评 此题主要考查了坐标与图形性质以及勾股定理和角平分线的性质等知识,利用勾股定理得出各线段长是解题关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 如图,已知M,N是线段AB上的两点,则AN=AM+MN=AB-NB,AN+MB-AB=MN,AM+MB-AN=NB.
如图,已知M,N是线段AB上的两点,则AN=AM+MN=AB-NB,AN+MB-AB=MN,AM+MB-AN=NB.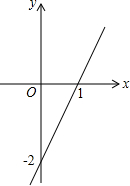 已知一个正比例函数平移后的图象如图中的直线y=kx+b所示.
已知一个正比例函数平移后的图象如图中的直线y=kx+b所示.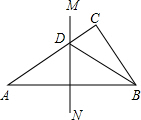 如图,在△ABC中,∠C=90°,AC=1cm,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD,若CD:DB=3:5,求CD的长和△ABC的面积.
如图,在△ABC中,∠C=90°,AC=1cm,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD,若CD:DB=3:5,求CD的长和△ABC的面积.