题目内容
2.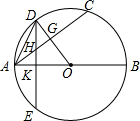 如图,AB是⊙O的直径,AC为⊙O的弦,半径0D⊥AC于G.弦DE⊥AB于K,交AC于H.
如图,AB是⊙O的直径,AC为⊙O的弦,半径0D⊥AC于G.弦DE⊥AB于K,交AC于H.(1)求证:AC=DE;
(2)求证:DH=AH;
(3)若DH=5,HE=11,求⊙O的半径.
分析 (1)根据垂径定理得到$\widehat{AD}=\widehat{CD}$,$\widehat{AD}=\widehat{AE}$,于是得到$\widehat{DE}=\widehat{AC}$,即可得到结论;
(2)由$\widehat{AD}=\widehat{CD}$,$\widehat{AD}=\widehat{AE}$,等量代换得到$\widehat{CD}=\widehat{AE}$,根据圆周角定理得到∠DAH=∠ADH,于是得到结论;
(3)连接AE,根据垂径定理得到DK=8,通过△ADE∽△ADH,得到$\frac{AD}{DE}=\frac{DH}{AD}$,求出AD=$\sqrt{DE•DH}$=4$\sqrt{5}$,由勾股定理得到AK=$\sqrt{A{D}^{2}-D{K}^{2}}$=4,于是得到结论.
解答 (1)证明:∵半径0D⊥AC于G,
∴$\widehat{AD}=\widehat{CD}$,
∵DE⊥AB于K,
∴$\widehat{AD}=\widehat{AE}$,
∴$\widehat{DE}=\widehat{AC}$,
∴AC=DE;
(2)证明:∵$\widehat{AD}=\widehat{CD}$,$\widehat{AD}=\widehat{AE}$,
∴$\widehat{CD}=\widehat{AE}$,
∴∠DAH=∠ADH,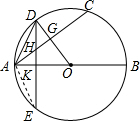
∴DH=AH;
(3)解:连接AE,
∵DH=5,HE=11,
∴DE=16,
∴DK=8,
∵∠AED=∠DAC,∠ADH=∠ADE,
∴△ADE∽△ADH,
∴$\frac{AD}{DE}=\frac{DH}{AD}$,
∴AD=$\sqrt{DE•DH}$=4$\sqrt{5}$,
∴AK=$\sqrt{A{D}^{2}-D{K}^{2}}$=4,
∵OD2=OK2+DK2,
即OD2=(OD-4)2+82,
解得:OD=10,
∴⊙O的半径=10.
点评 本题考查了垂径定理,圆周角定理,勾股定理,相似三角形的判定和性质,正确的作出辅助线构造相似三角形是解题的关键.

 如图,已知M,N是线段AB上的两点,则AN=AM+MN=AB-NB,AN+MB-AB=MN,AM+MB-AN=NB.
如图,已知M,N是线段AB上的两点,则AN=AM+MN=AB-NB,AN+MB-AB=MN,AM+MB-AN=NB.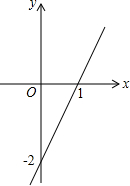 已知一个正比例函数平移后的图象如图中的直线y=kx+b所示.
已知一个正比例函数平移后的图象如图中的直线y=kx+b所示.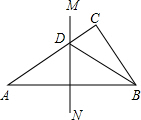 如图,在△ABC中,∠C=90°,AC=1cm,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD,若CD:DB=3:5,求CD的长和△ABC的面积.
如图,在△ABC中,∠C=90°,AC=1cm,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD,若CD:DB=3:5,求CD的长和△ABC的面积.