题目内容
二次函数y=ax2+bx+c(a>0,b<0)的图象和x轴,y轴都只有一个交点,它们分别为P、Q,已知|PQ|=2
,且有b+2bc=0,另一个一次函数y=x+m的图象过P点,并与这个二次函数图象交于另一点R,求△PQR的面积.
| 2 |
考点:抛物线与x轴的交点
专题:
分析:根据图象与x轴只有一个交点,可得△等于零,解方程组,可得a、b、c的值,可得函数解析式,再解方程组,可得交点坐标,根据三角形的面积公式,可得答案.
解答:解:当x=0时,y=c,二次函数与y轴的交点Q(0,c),二次函数y=ax2+bx+c(a>0,b<0)的图象和x轴只有一个交点,
∴b2-4ac=0 ①
∴x=
,与x轴的交点P的坐标是(-
,0).
∵|PQ|=
=
=2
,
∴c2+
=8 ②,又∵b+2bc=0 ③,
①②③联立得方程组
由①得2ac=
④,
把④代入③得b+
=0,
解得 b=0不符合题意的要舍去)b=-2,
把b=-2代入②③得
,
解得
(不符合题意的要舍去),
∴抛物线的解析式是y=
x2-2x+2,
∴P(2,0)Q(0,2),
∵y=x+m的图象过P点,
m+2=0,解得m=-2,
直线解析式是y=x-2,
联立抛物线解析式,得
,
解得
,
R(4,2),
∴QR∥x,
∴S△PQR=
QR•Qy=
×4×2=4.
∴b2-4ac=0 ①
∴x=
| b |
| 2a |
| b |
| 2a |
∵|PQ|=
| OP2+OQ2 |
c2+(-
|
| 2 |
∴c2+
| b2 |
| 4a2 |
①②③联立得方程组
|
由①得2ac=
| b2 |
| 2 |
把④代入③得b+
| b2 |
| 2 |
解得 b=0不符合题意的要舍去)b=-2,
把b=-2代入②③得
|
解得
|
|
∴抛物线的解析式是y=
| 1 |
| 2 |
∴P(2,0)Q(0,2),
∵y=x+m的图象过P点,
m+2=0,解得m=-2,
直线解析式是y=x-2,
联立抛物线解析式,得
|
解得
|
R(4,2),
∴QR∥x,
∴S△PQR=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了抛物线与x轴的交点,利用了图象和x轴,y轴都只有一个交点,得出方程,消元解方程组,三角形的面积公式.

练习册系列答案
相关题目
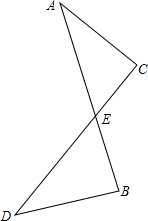 如图,已知AB与CD交于点E,AB与CD的夹角为45°,若∠B+∠C=225°,AC=3,DB=4,AB=5,求DC的长.
如图,已知AB与CD交于点E,AB与CD的夹角为45°,若∠B+∠C=225°,AC=3,DB=4,AB=5,求DC的长. 已知,如图在△ABC中,AD⊥BC于点D,BF平分∠ABC交AD于点E,且∠BED=∠C=64°,求证:△ABF≌△CBF.
已知,如图在△ABC中,AD⊥BC于点D,BF平分∠ABC交AD于点E,且∠BED=∠C=64°,求证:△ABF≌△CBF.