题目内容
 如图,已知△ABC为等边三角形,AB=3,以C为圆心,1为半径作圆,P为⊙C上一动点,连AP,并绕点A顺时针旋转60°到P′,连接CP′,则CP′的取值范围是
如图,已知△ABC为等边三角形,AB=3,以C为圆心,1为半径作圆,P为⊙C上一动点,连AP,并绕点A顺时针旋转60°到P′,连接CP′,则CP′的取值范围是考点:全等三角形的判定与性质,等边三角形的性质,圆的认识
专题:
分析:连接CP、BP′,根据同角的余角相等求出∠CAP=∠BAP′,然后利用“边角边”证明△APC和△AP′B全等,根据全等三角形对应边相等可得PC=P′B,再利用勾股定理列式求出BC,然后根据三角形的任意两边之和大于第三边,两边之差小于第三边求解即可.
解答: 解:如图,连接CP、BP′,
解:如图,连接CP、BP′,
∵∠BAC=60°,旋转角为60°,
∴∠CAP+∠CAP′=∠BAP′+∠CAP′=60°,
∴∠CAP=∠BAP′,
在△APC和△AP′B中,
,
∴△APC≌△AP′B(SAS),
∴PC=P′B=1,
∵BC=AB=AC=3,
在△BCP′中,有2<CP′<4,
当三点共线时取到等号,此时不是三角形,但符合题意.
所以,CP′的取值范围是:2≤CP′≤4.
故答案为:2≤CP′≤4.
 解:如图,连接CP、BP′,
解:如图,连接CP、BP′,∵∠BAC=60°,旋转角为60°,
∴∠CAP+∠CAP′=∠BAP′+∠CAP′=60°,
∴∠CAP=∠BAP′,
在△APC和△AP′B中,
|
∴△APC≌△AP′B(SAS),
∴PC=P′B=1,
∵BC=AB=AC=3,
在△BCP′中,有2<CP′<4,
当三点共线时取到等号,此时不是三角形,但符合题意.
所以,CP′的取值范围是:2≤CP′≤4.
故答案为:2≤CP′≤4.
点评:本题考查了全等三角形的判定与性质,等腰直角三角形的性质,圆的认识,三角形的三边关系,熟记各性质并作辅助线构造成全等三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知a,b分别是矩形ABCD的两边,且满足a=
+
+4,若矩形的两条对角线相交所构成的锐角为α.则tanα的值为( )
| 3-b |
| b-3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
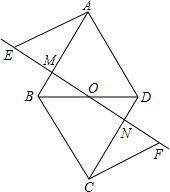 如图,O为四边形ABCD的对角线BD的中点,过点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF,AE∥CF,AE=CF.求证:四边形ABCD是平行四边形.
如图,O为四边形ABCD的对角线BD的中点,过点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF,AE∥CF,AE=CF.求证:四边形ABCD是平行四边形. 如图:是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对面上的汉字是
如图:是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对面上的汉字是 如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形ODEF,则E的坐标为
如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形ODEF,则E的坐标为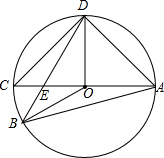 如图,AC为⊙O的直径,AC=4,B、D分别在AC两侧的圆上,∠BAD=60°,BD与AC的交点为E.
如图,AC为⊙O的直径,AC=4,B、D分别在AC两侧的圆上,∠BAD=60°,BD与AC的交点为E.