题目内容
 已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm.点P由B出发沿BA方向向点A匀速运动;点Q由A出发沿AC方向向点C匀速运动;连接PQ.若设BP=x cm,AQ=2x cm(0<x<2),解答下列问题:
已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm.点P由B出发沿BA方向向点A匀速运动;点Q由A出发沿AC方向向点C匀速运动;连接PQ.若设BP=x cm,AQ=2x cm(0<x<2),解答下列问题:(1)当x为何值时,PQ∥BC?
(2)设△AQP的面积为y( cm2),求y与x之间的函数关系式;
(3)是否存在x的值,使线段PQ恰好把Rt△ACB面积平分?若存在,求出此时x的值;若不存在,说明理由.
考点:一元二次方程的应用,函数关系式,相似三角形的判定与性质
专题:几何动点问题
分析:(1)由勾股定理得出AB,因为AP=5-x,AQ=2x,则可证明△APQ∽△ABC,即可求得x;
(2)过点P作PH⊥AC于H.由△APH∽△ABC,得PH=3-
x,然后根据三角形的面积公式,从而求得y与t的函数关系式;
(3)由线段PQ恰好把△ABC的面积平分,列出一元二次方程,解方程即可.
(2)过点P作PH⊥AC于H.由△APH∽△ABC,得PH=3-
| 3 |
| 5 |
(3)由线段PQ恰好把△ABC的面积平分,列出一元二次方程,解方程即可.
解答:解:(1)在Rt△ABC中,AB=
=5,
由题意知:AP=5-x,AQ=2x,
若PQ∥BC,则△APQ∽△ABC,
∴
=
,
∴
=
,
解得:x=
.
故当x=
秒时,PQ∥BC;
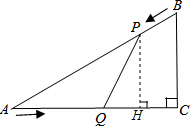 (2)如图,过点P作PH⊥AC于H.
(2)如图,过点P作PH⊥AC于H.
∵∠C=90°,
∴AC⊥BC,
∴PH∥BC,
∴△APH∽△ABC,
∴
=
,
∴
=
,
∴PH=3-
x,
∴△AQP的面积为:
y=
×AQ×PH
=
×2x×(3-
x)
=-
x2+3x,
即y=-
x2+3x;
 (2)存在某时刻t,使线段PQ恰好把△ABC的面积平分,理由为:
(2)存在某时刻t,使线段PQ恰好把△ABC的面积平分,理由为:
假设存在某时刻x,使线段PQ恰好把△ABC的面积平分,
有S△AQP=
S△ABC,而S△ABC=
AC•BC=6(cm2),
则此时S△AQP=3(cm2),-
x2+3x=3,
化简得:x2-5x+5=0,
∵△=(-5)2-4×1×5=5,
∴x=
,
∵0<x<2,
∴x=
.
则存在x=
,使线段PQ恰好把△ABC的面积平分.
| BC2+AC2 |
由题意知:AP=5-x,AQ=2x,
若PQ∥BC,则△APQ∽△ABC,
∴
| AQ |
| AC |
| AP |
| AB |
∴
| 2x |
| 4 |
| 5-x |
| 5 |
解得:x=
| 10 |
| 7 |
故当x=
| 10 |
| 7 |
 (2)如图,过点P作PH⊥AC于H.
(2)如图,过点P作PH⊥AC于H.∵∠C=90°,
∴AC⊥BC,
∴PH∥BC,
∴△APH∽△ABC,
∴
| PH |
| BC |
| AP |
| AB |
∴
| PH |
| 3 |
| 5-x |
| 5 |
∴PH=3-
| 3 |
| 5 |
∴△AQP的面积为:
y=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 5 |
=-
| 3 |
| 5 |
即y=-
| 3 |
| 5 |
 (2)存在某时刻t,使线段PQ恰好把△ABC的面积平分,理由为:
(2)存在某时刻t,使线段PQ恰好把△ABC的面积平分,理由为:假设存在某时刻x,使线段PQ恰好把△ABC的面积平分,
有S△AQP=
| 1 |
| 2 |
| 1 |
| 2 |
则此时S△AQP=3(cm2),-
| 3 |
| 5 |
化简得:x2-5x+5=0,
∵△=(-5)2-4×1×5=5,
∴x=
5±
| ||
| 2 |
∵0<x<2,
∴x=
5-
| ||
| 2 |
则存在x=
5-
| ||
| 2 |
点评:此题主要考查了一元二次方程的应用,相似三角形的判定与性质以及二次函数的最值问题以及勾股定理等知识,利用相似三角形的性质得出PH的长是解题关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知a,b分别是矩形ABCD的两边,且满足a=
+
+4,若矩形的两条对角线相交所构成的锐角为α.则tanα的值为( )
| 3-b |
| b-3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
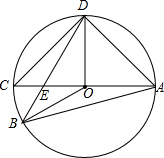 如图,AC为⊙O的直径,AC=4,B、D分别在AC两侧的圆上,∠BAD=60°,BD与AC的交点为E.
如图,AC为⊙O的直径,AC=4,B、D分别在AC两侧的圆上,∠BAD=60°,BD与AC的交点为E.
 如图,在矩形AB CD中,点M、N分别在AD、BC边上,且AM=CN.
如图,在矩形AB CD中,点M、N分别在AD、BC边上,且AM=CN. 已知二次函数C1:y=x2+2ax+2x-a+1,且a变化时,二次函数C1的图象顶点M总在抛物线C2上;
已知二次函数C1:y=x2+2ax+2x-a+1,且a变化时,二次函数C1的图象顶点M总在抛物线C2上;