题目内容
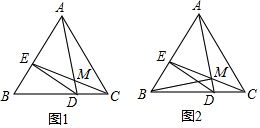
4.△ABC是边长为6的等边三角形,D、E是AB、BC上的动点,且BE=DC,连AD、EC交于点M.(1)求证:△AME∽△ABD;
(2)连DE,若BD=2DC,求证:①DE⊥AB;②连BM,求BM的长;
(3)当D、E在△ABC的边BC、AB上运动时,直接写出△AMC的面积的最大值.
分析 (1)根据等边三角形性质得出AB=BC,∠ABD=∠C=60°,可得△ABD≌△BCE;推出∠BAD=∠CBE,再通过三角形外角性质即可求出∠AME的度数,即可得出结论.
(2)①过点C作CF⊥AB于F,判断出△BDE∽△BCF,即可得出结论,
②先利用勾股定理求出AD,AM,再用相似得出比例式求出MN,AN最后用勾股定理即可得出BM.
(3)先判断出△ACM面积最大时,点M的位置,最后用圆的性质即可求出结论.
解答 解::①∵△ABC为等边三角形,
∴AB=BC,∠ABD=∠C=60°,
在△ABD和△BCE中,$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠C}\\{BD=CE}\end{array}\right.$
∴△ABD≌△BCE(SAS),
∴AD=BE.∠BAD=∠CBE,
∴∠AME=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC=60°=∠B
∵∠EAM=∠DAB,
∴△AME∽△ABD,
(2)如图1, 过点C作CF⊥AB,
过点C作CF⊥AB,
∴∠BFC=90°
∵△ABC是边长为6的等边三角形,
∴AB=BC=6,BF=$\frac{1}{2}$AB=3,
∵BD=2DC,
∴CD=2,BD=4
∴BE=CD=2,
∵$\frac{BE}{BF}=\frac{2}{3}$,$\frac{BD}{BC}=\frac{4}{6}=\frac{2}{3}$,
∴$\frac{BE}{BF}=\frac{BD}{BC}$,
∵∠B=∠B,
∴△BDE∽△BCF,
∴∠BED=∠BFC=90°,
∴DE⊥AB,
如图2,
过点A作AH⊥BC,
∴BH=$\frac{1}{2}$BC=3,
∴DH=BD-BH=1,AH=3$\sqrt{3}$,
根据勾股定理得,AD=$\sqrt{A{H}^{2}+D{H}^{2}}$=2$\sqrt{7}$,
由(1)知,△AME∽△ABD,
∴$\frac{AM}{AB}=\frac{AE}{AD}=\frac{EM}{BD}$,
∴$\frac{AM}{6}=\frac{4}{2\sqrt{7}}=\frac{EM}{4}$,
∴AM=$\frac{12\sqrt{7}}{7}$
在Rt△BDE中,DE=$\sqrt{B{D}^{2}-B{E}^{2}}$=2$\sqrt{3}$,
过点M作MN⊥AB,
∵DE⊥AB,
∴DE∥MN,
∴$\frac{MN}{DE}=\frac{AM}{AD}$=$\frac{AN}{AE}$
∴$\frac{MN}{2\sqrt{3}}=\frac{\frac{12\sqrt{7}}{7}}{2\sqrt{7}}=\frac{AN}{4}$,
∴MN=$\frac{12\sqrt{3}}{7}$,AN=$\frac{24}{7}$
∴BN=AB-AN=$\frac{18}{7}$
在Rt△BMN中,BM=$\sqrt{B{N}^{2}+M{N}^{2}}$=$\frac{6\sqrt{21}}{7}$.
(3)如图3,
由(1)可知∠AME=∠B=60°,
∴∠AMC=120°,点M的轨迹是一段弧,它所对的弦AC对的圆心角120°,
∴△AMC的AC边上的高为M到AC的距离,最大距离即为弓形的高IG,
在Rt△AOI中,AI=3,∠AOI=$\frac{1}{2}$∠AOC=60°,
∴OA=2$\sqrt{3}$,OI=$\sqrt{3}$,
∴IG=$\sqrt{3}$,
∴S△AMC最大=$\frac{1}{2}$×AC×IG=$\frac{1}{2}$×6×$\sqrt{3}$=3$\sqrt{3}$.
点评 此题是相似形综合题,主要考查了相似三角形的判定和性质,平行线分线段成比例定理,极值,圆的性质,解本题的关键是判断出△BDE∽△BCF.

 如图,已知反比例函数y=$\frac{k}{x}$(x>0)的图象如图所示,则k的取值范围是( )
如图,已知反比例函数y=$\frac{k}{x}$(x>0)的图象如图所示,则k的取值范围是( )| A. | -2<k<-1 | B. | -3<k<-2 | C. | -4<k<-3 | D. | -5<k<-4 |
| A. | 168×103 | B. | 16.8×104 | C. | 1.68×105 | D. | 0.168×106 |

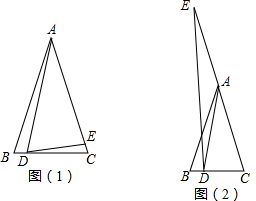
 已知线段a、b以及∠α,求作△ABC,使得AB+AC=a,且BC=b,∠A=∠α.
已知线段a、b以及∠α,求作△ABC,使得AB+AC=a,且BC=b,∠A=∠α.