题目内容
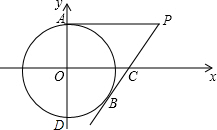 如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,D点P(2
如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,D点P(2| 3 |
(1)证明PA是⊙O的切线;
(2)当点B在第四象限且PB与⊙O相切时,求点B的坐标;
(3)在(2)的条件下求直线AB的解析式.并直接写出PB与⊙O相切时点B运动的时间.
考点:圆的综合题
专题:综合题
分析:(1)证明AP∥x轴,得出∠OAP=90°,可得出结论;
(2)连接OP,OB,作PE⊥x轴于点E,BF⊥x轴于点F,易证△OBC≌△PEC,得出OC=PC,设OC=PC=x,则CE=OE-OC=2
-x,在Rt△PCE中利用勾股定理可求出x的值,再由△OBC面积的两种表示形式求出BF,在Rt△OFB中求出OF,继而可得点B的坐标;
(3)求出∠BOF、BOD的度数,求出弧长BD的长度,可得点B运动的时间.
(2)连接OP,OB,作PE⊥x轴于点E,BF⊥x轴于点F,易证△OBC≌△PEC,得出OC=PC,设OC=PC=x,则CE=OE-OC=2
| 3 |
(3)求出∠BOF、BOD的度数,求出弧长BD的长度,可得点B运动的时间.
解答:(1)证明:∵A(0,2),P(2
,2),
∴AP∥x轴,
∴∠OAP=90°,且点A在⊙O上,
∴PA是⊙O的切线;
(2)解:连接OP,OB,作PE⊥x轴于点E,BF⊥x轴于点F,
∵PB切⊙O于点B,
∴∠OBP=90°,即∠OBP=∠PEC,
又∵OB=PE=2,∠OCB=∠PCE,
∴△OBC≌△PEC,
∴OC=PC,
设OC=PC=x,则CE=OE-OC=2
-x,
在Rt△PCE中,∵PC2=CE2+PE2,
∴x2=(2
-x)2+22,
解得:x=
,
∴BC=CE=2
-
=
∵
OB•BC=
OC•BF,即
×2×
=
×
×BF,
∴BF=1,
∴OF=
=
=
,
由点B在第四象限可知B(
,-1);
(3)解:设直线AB的解析式为y=kx+b,
由A(0,2),B,(
,-1);可得
;
解得:
,
∴直线AB的解析式为y=-
x+2,
∵tan∠BOF=
=
,
∴∠BOF=30°,
∴∠BOD=60°,
∴l
=
=
π,
∴此时点B运动了
π秒.
| 3 |
∴AP∥x轴,
∴∠OAP=90°,且点A在⊙O上,
∴PA是⊙O的切线;
(2)解:连接OP,OB,作PE⊥x轴于点E,BF⊥x轴于点F,

∵PB切⊙O于点B,
∴∠OBP=90°,即∠OBP=∠PEC,
又∵OB=PE=2,∠OCB=∠PCE,
∴△OBC≌△PEC,
∴OC=PC,
设OC=PC=x,则CE=OE-OC=2
| 3 |
在Rt△PCE中,∵PC2=CE2+PE2,
∴x2=(2
| 3 |
解得:x=
| 4 |
| 3 |
| 3 |
∴BC=CE=2
| 3 |
| 4 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
| 3 |
∴BF=1,
∴OF=
| OB2-BF2 |
| 22-12 |
| 3 |
由点B在第四象限可知B(
| 3 |
(3)解:设直线AB的解析式为y=kx+b,
由A(0,2),B,(
| 3 |
|
解得:
|
∴直线AB的解析式为y=-
| 3 |
∵tan∠BOF=
| BF |
| OF |
| ||
| 3 |
∴∠BOF=30°,
∴∠BOD=60°,
∴l
 |
| BD |
| 60π×2 |
| 180 |
| 2 |
| 3 |
∴此时点B运动了
| 2 |
| 3 |
点评:本题考查了圆的综合,涉及了切线的判定、待定系数法求函数解析式、弧长的计算及三角形的面积,解答此类综合性较强的题目,要求同学们熟练基本知识的掌握,并能将所学知识融会贯通.

练习册系列答案
相关题目
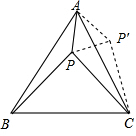 如图,等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5,则∠APB=
如图,等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5,则∠APB=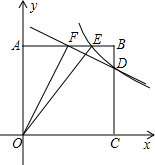 如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).
如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).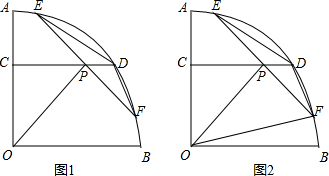 如图1,在半径为5的扇形AOB中,∠AOB=90°,点C、D分别在半径OA与弧AB上,且AC=2,CD平行OB,点P是CD上一动点,过P作PO的垂线交弧AB于点E、F,联结DE、BF.
如图1,在半径为5的扇形AOB中,∠AOB=90°,点C、D分别在半径OA与弧AB上,且AC=2,CD平行OB,点P是CD上一动点,过P作PO的垂线交弧AB于点E、F,联结DE、BF. 如图,在平面直角坐标系中,O为原点,直线y=
如图,在平面直角坐标系中,O为原点,直线y=