��Ŀ����
18����ͼ���Ƕ��κ���y=��x+m��2+k��ͼ���䶥������ΪM��1��-4������1�����ͼ����x��Ľ���A��B�����ꣻ
��2���ڶ��κ�����ͼ�����Ƿ���ڵ�P��ʹS��PAB=$\frac{5}{4}$S��MAB�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��3�������κ�����ͼ����x���·��IJ�����x�ᷭ�ۣ�ͼ������ಿ�ֱ��ֲ��䣬�õ�һ���µ�ͼ����ͼ�ڣ������������ͼ��ش�ֱ��y=x+b��b��1�����ͼ������������������ʱ��b��ȡֵ��Χ��

���� ��1���ɶ�������ȷ��m��k��ֵ������y=0���ͼ����x��Ľ������ꣻ
��2�������������P�㣬���ڵױ���ͬ�������PAB�ĸ�|y|����y���������κ�������ʽ���P�����ꣻ
��3��������ת���µĺ���ͼ����ֱ��y=x+b��b��1ȷ����ֱ���ƶ��ķ�Χ�����b��ȡֵ��Χ��
��� �⣺��1����ΪM��1��-4���Ƕ��κ���y=��x+m��2+k�Ķ������꣬
����y=��x-1��2-4=x2-2x-3��
��x2-2x-3=0��
��֮��x1=-1��x2=3��
��A��B���������ֱ�ΪA��-1��0����B��3��0����
��2���ڶ��κ�����ͼ���ϴ��ڵ�P��ʹS��PAB=$\frac{5}{4}$S��MAB��
��P��x��y����
��S��PAB=$\frac{1}{2}$|AB|��|y|=2|y|
�֡�S��MAB=$\frac{1}{2}$|AB|��|-4|=8��
��2|y|=$\frac{5}{4}$��
��y=��5��
�߶��κ�������СֵΪ-4��
��y=5��
��y=5ʱ��x=-2��x=4��
��P��������-2��5����4��5��
��3������ͼ����ֱ��y=x+b����A��-1��0��ʱ-1+b=0��
�ɵ�b=1������Ϊb��1��
�ʿ�֪y=x+b��y=x+1���·���
��ֱ��y=x+b������B��3��0��ʱ��3+b=0����b=-3��
��ͼ��֪�����������b��ȡֵ��ΧΪ-3��b��1ʱ��ֱ��y=x+b���ͼ�������������㣮
�ڵ�ֱ����M���Ϸ�ʱҲ�������⣬��ʱb��$\frac{13}{4}$��
��b��ȡֵ��ΧΪ��-3��b��1��b��$\frac{13}{4}$��
���� ���⿼�����ɺ���ͼ��ȷ�����꣬�Լ����������ϵ���������ֱ����ͼ��Ľ������⣬�ۺ����������ν�ϵ�˼�룮

| A�� | ���鴺����������������� | |
| B�� | ѡ��ijУ��������ѧ���μ�ȫ������ | |
| C�� | ���ij��������� | |
| D�� | Ь�����������Ь���ܳ��ܵ����۴��� |
 ��ͼ���������չ��ͼ����ԭ����������������ϵ�����֮�͵���Сֵ��6��
��ͼ���������չ��ͼ����ԭ����������������ϵ�����֮�͵���Сֵ��6��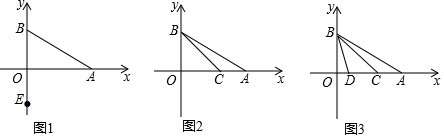




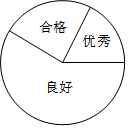 ijУѧ���μ�ij����ѧ���ijɼ�����Ϊ���㡢���á��ϸ������ȼ�����������Ϊ2��7��3����ͼ��ʾ������ͼ��ʾ�����ֲ������
ijУѧ���μ�ij����ѧ���ijɼ�����Ϊ���㡢���á��ϸ������ȼ�����������Ϊ2��7��3����ͼ��ʾ������ͼ��ʾ�����ֲ������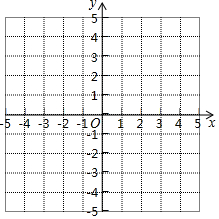 ��֪��ABC���������������ֱ���A��-2��3������B��0��1������C��2��2����
��֪��ABC���������������ֱ���A��-2��3������B��0��1������C��2��2����