题目内容
8.学习完分式及其运算后,李明同学在纠错本中积累了这样一个题目:先化简代数式(1-$\frac{3}{a+2}$)÷$\frac{{a}^{2}-2a+1}{{a}^{2}-4}$,再从-2,2,0三个数中选一个适当的数作为a的值代入求值,这道题你会吗?试试看!分析 根据分式的运算法则即可求出答案.
解答 解:原式=$\frac{a-1}{a+2}$×$\frac{(a-2)(a+2)}{(a-1)^{2}}$
=$\frac{a-2}{a-1}$
由于$\left\{\begin{array}{l}{a+2≠0}\\{{a}^{2}-4≠0}\\{a-1≠0}\end{array}\right.$
解得:a≠±2且a≠1
令a=0代入$\frac{a-2}{a-1}$
∴原式=2
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
相关题目
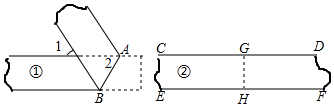
18.一次数学活动中,检验两条纸带①、②的边线是否平行,小明和小丽采用两种不同的方法:小明对纸带①沿AB折叠,量得∠1=∠2=50°;小丽对纸带②沿GH折叠,发现GD与GC重合,HF与HE重合.则下列判断正确的是( )

| A. | 纸带①的边线平行,纸带②的边线不平行 | |
| B. | 纸带①的边线不平行,纸带②的边线平行 | |
| C. | 纸带①、②的边线都平行 | |
| D. | 纸带①、②的边线都不平行 |
17.一组数据:1,2,3,4,10的方差为( )
| A. | 4 | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | 10 |





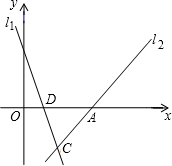 如图,已知直线l1:y=-3x+3与直线l2:y=mx-4m的图象的交点C在第四象限,且点C到y轴的距离为2.
如图,已知直线l1:y=-3x+3与直线l2:y=mx-4m的图象的交点C在第四象限,且点C到y轴的距离为2.