题目内容
7.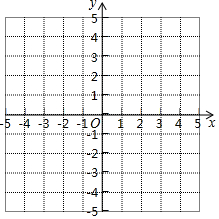 已知△ABC的三个顶点的坐标分别是A(-2,3),点B(0,1),点C(2,2).
已知△ABC的三个顶点的坐标分别是A(-2,3),点B(0,1),点C(2,2).(1)在所给的平面直角坐标系中画出△ABC.
(2)直接写出点A到x轴,y轴的距离分别是多少?
(3)求出△ABC的面积.
分析 (1)根据点A、B、C的坐标描点,连接三点从而可得到△ABC;
(2)根据A得坐标即可得出结论;
(3)根据三角形面积公式计算;
解答 解:(1)如图,△ABC为所作;
(2)由图可知,点A(-2,3)到x轴的距离为3,到y轴的距离为2.
(3)△ABC的面积=4×2-$\frac{1}{2}$×2×2-$\frac{1}{2}$×2×1-$\frac{1}{2}$×4×1=3.
点评 本题考查了坐标与图形性质,主要是在平面直角坐标系中确定点的位置的方法和三角形的面积的求解.

练习册系列答案
相关题目
17.一组数据:1,2,3,4,10的方差为( )
| A. | 4 | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | 10 |
15.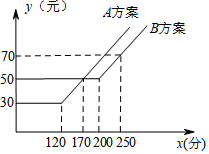 如图,某电脑公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分钟)之间的关系,则以下说法错误的是( )
如图,某电脑公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分钟)之间的关系,则以下说法错误的是( )
 如图,某电脑公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分钟)之间的关系,则以下说法错误的是( )
如图,某电脑公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分钟)之间的关系,则以下说法错误的是( )| A. | 若通话时间少于120分,则A方案比B方案便宜20元 | |
| B. | 若通讯费用为60元,则B方案比A方案的通话时间多 | |
| C. | 若两种方案通讯费用相差10元,则通话时间是145分或185分 | |
| D. | 若通话时间超过200分,则B方案比A方案便宜12元 |
12. 如图,在平面直角坐标系中,A(0,0)、B(4,0)、D(1,2)为平行四边形的三个顶点,则第四个顶点C的坐标是( )
如图,在平面直角坐标系中,A(0,0)、B(4,0)、D(1,2)为平行四边形的三个顶点,则第四个顶点C的坐标是( )
 如图,在平面直角坐标系中,A(0,0)、B(4,0)、D(1,2)为平行四边形的三个顶点,则第四个顶点C的坐标是( )
如图,在平面直角坐标系中,A(0,0)、B(4,0)、D(1,2)为平行四边形的三个顶点,则第四个顶点C的坐标是( )| A. | (2,5) | B. | (4,2) | C. | (5,2) | D. | (6,2) |
16.已知多项式A与2x2+5x的和等于2x2-3x+1,则这个多项式为( )
| A. | 2x-1 | B. | 2x+1 | C. | -8x+1 | D. | -8x-1 |
17.在下列代数式中,次数为3的单项式是( )
| A. | 3x2 | B. | -x2y | C. | x3+1 | D. | x3y |

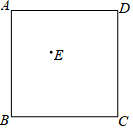 如图,在正方形ABCD内任取一点E,连结AE、BE,在△ABE外分别以AE、BE为边作正方形AEMN和EBFG.
如图,在正方形ABCD内任取一点E,连结AE、BE,在△ABE外分别以AE、BE为边作正方形AEMN和EBFG. 如图是一次函数y=mx+n的图象,则关于x的不等式mx+n>2的解集是x>0.
如图是一次函数y=mx+n的图象,则关于x的不等式mx+n>2的解集是x>0.