题目内容
3.观察下列方程的特征及其解的特点;①x+$\frac{2}{x}$=-3的解为x1=-1,x2=-2.
②x+$\frac{6}{x}$=-5的解为x1=-2,x2=-3.
③x+$\frac{12}{x}$=-7的解为x1=-3,x2=-4;
解答下列问题;
(1)请你写出一个符合上述特征的方程为x+$\frac{20}{x}$=-9,其解为x1=-4,x2=-5.
(2)根据这类方程特征,写出第n个方程为x+$\frac{{n}^{2}+n}{x}$=-2n-1,其解为x1=-n,x2=-n-1.
(3)请利用(2)的结论,求关于x的方程x+$\frac{{n}^{2}+n}{x+3}$=-2(n+2)(其中n为正整数)的解.
分析 (1)观察阅读材料中的方程解过程,归纳总结得到结果;
(2)仿照方程解方程,归纳总结得到结果;
(3)方程变形后,利用得出的规律得到结果即可.
解答 解:(1)x+$\frac{20}{x}=-9$,其解为:x1=-4,x2=-5,
故答案为:x+$\frac{20}{x}$=-9,x1=-4,x2=-5;
(2)x+$\frac{{n}^{2}+n}{x}$=-(2n+1),其解为:x1=-n,x2=-n-1,
故答案为:x+$\frac{{n}^{2}+n}{x}$=-(2n+1),x1=-n,x2=-n-1;
(3)x+$\frac{{n}^{2}+n}{x+3}$=-2(n+2)
x+3+$\frac{{n}^{2}+n}{x+3}$=-2(n+2)+3
(x+3)+$\frac{{n}^{2}+n}{x+3}$=-(2n+1)
∴x+3=-n或x+3=-(n+1)
即:x1=-n-3,x2=-n-4.
点评 此题考查了分式方程的解,方程的解即为能使方程左右两边相等的未知数的值.弄清题中的规律是解本题的关键.

练习册系列答案
相关题目
 如图,搭一个小正方形需要4根火柴棒,搭2个小正方形需要7根火柴棒,…搭70个小正方形,需要211个火柴棒.
如图,搭一个小正方形需要4根火柴棒,搭2个小正方形需要7根火柴棒,…搭70个小正方形,需要211个火柴棒.
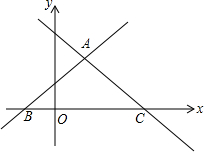 如图,在平面直角坐标系中,直线y=x+1与直线y=-$\frac{3}{4}$x+3,交于点A($\frac{8}{7}$,$\frac{15}{7}$),且两直线分别交x轴于B,C两点.
如图,在平面直角坐标系中,直线y=x+1与直线y=-$\frac{3}{4}$x+3,交于点A($\frac{8}{7}$,$\frac{15}{7}$),且两直线分别交x轴于B,C两点. 如图所示,AB,CD相交于O点,OE是∠COB的平分线,FO⊥OE,且∠AOD=60°.
如图所示,AB,CD相交于O点,OE是∠COB的平分线,FO⊥OE,且∠AOD=60°.