题目内容
19. 如图,在△ABC中,AD是∠BAC的角平分线,AB=6cm,AC=8cm,则S△ABD:S△ACD=3:4,BD:CD=3:4.
如图,在△ABC中,AD是∠BAC的角平分线,AB=6cm,AC=8cm,则S△ABD:S△ACD=3:4,BD:CD=3:4.
分析 根据角平分线上的点到角的两边距离相等可得点D到AB、AC的距离相等,再根据等高的三角形的面积的比等于底边的比求解.
解答 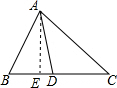 解:∵AD是∠BAC的角平分线,
解:∵AD是∠BAC的角平分线,
∴点D到AB、AC的距离相等,
∴S△ABD:S△ACD=6:8=3:4,
过A作AE⊥BC于E,
∴S△ABD=$\frac{1}{2}$BD•AE,S△ACD=$\frac{1}{2}$CD•AE,
∴BD:CD=S△ABD:S△ACD=3:4.
故答案为:3:4.3:4.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,等高的三角形的面积的比等于底边的比,熟记性质与等高的三角形的面积的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 实数a,b在数轴上对应的位置,如图所示:则|a-b|-|b|等于( )
实数a,b在数轴上对应的位置,如图所示:则|a-b|-|b|等于( )
 实数a,b在数轴上对应的位置,如图所示:则|a-b|-|b|等于( )
实数a,b在数轴上对应的位置,如图所示:则|a-b|-|b|等于( )| A. | a | B. | a-2b | C. | -a | D. | b-a |
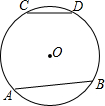 如图,已知A,B,C,D为圆O上的四点,且$\widehat{AB}$=2$\widehat{CD}$,请判断AB与2CD是否相等,说明理由.
如图,已知A,B,C,D为圆O上的四点,且$\widehat{AB}$=2$\widehat{CD}$,请判断AB与2CD是否相等,说明理由.