题目内容
3.如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.(1)问t为何值时,△ABP是等腰三角形?
(2)问t为何值时,点P与所在边对角顶点连线正好平分所在边的对角?
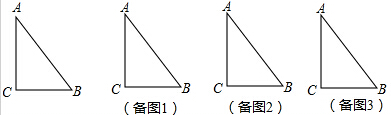
分析 (1)根据勾股定理求出AC的长,由题意可知,只有当点P在AC上时,△ABP可能为等腰三角形,设PC=x,则AP=BP=8-x,再由勾股定理求出x的值即可;
(2)分点P在∠ABC,∠ACB与∠BAC的平分线上三种情况进行讨论.
解答  解:(1)∵△ABC中,∠C=90°,AB=10cm,BC=6cm,
解:(1)∵△ABC中,∠C=90°,AB=10cm,BC=6cm,
∴AC=$\sqrt{{AB}^{2}-{BC}^{2}}$=$\sqrt{{10}^{2}-{6}^{2}}$=8cm.
如图1所示,设PC=x,则AP=BP=8-x,
在Rt△PCB中,BC2+PC2=PB2,即62+x2=(8-x)2,解得x=$\frac{7}{4}$,
∵速度为每秒1cm,
∴t=$\frac{7}{4}$秒;
(2)如图2,当点P在∠ABC的平分线上时,过点P作PE⊥AB,则CP=PE,
设CP=PE=x,则S△ABP=S△ABC-S△BCP,即$\frac{1}{2}$×10x=$\frac{1}{2}$×6×8-$\frac{1}{2}$×6x,解得x=3,故t=3秒;
如图3,当点P在∠ACB的平分线上时,过点D作DE⊥AC,DF⊥BC,则DE=DF,
设DE=DF=h,则S△ACP=S△ABC-S△BCP,即$\frac{1}{2}$×8h=$\frac{1}{2}$×6×8-$\frac{1}{2}$×6h,解得h=$\frac{24}{7}$,
∵∠ACB=90°,
∴CE=PE=$\frac{24}{7}$,
∴AE=8-$\frac{24}{7}$=$\frac{32}{7}$,
∴AP=$\sqrt{{AE}^{2}+{PE}^{2}}$=$\sqrt{{(\frac{32}{7})}^{2}+{(\frac{24}{7})}^{2}}$=$\frac{40}{7}$,
∴AC+AP=8+$\frac{40}{7}$=$\frac{96}{7}$(cm),
∴t=$\frac{96}{7}$秒;
如图4所示,当P在∠BAC的平分线上时,过点P作PE⊥AB,则PC=PE,
设PC=PE=h,则S△ABP=S△ABC-S△ACP,即$\frac{1}{2}$×10h=$\frac{1}{2}$×6×8-$\frac{1}{2}$×8h,解得h=$\frac{8}{3}$,
∴AB+AC+BP=10+8+(6-$\frac{8}{3}$)=$\frac{64}{3}$(cm),
∴t=$\frac{64}{3}$秒.
综上所述,当t=3秒,$\frac{96}{7}$秒或$\frac{64}{3}$秒时,点P与所在边对角顶点连线正好平分所在边的对角.
点评 本题考查的是相似形综合题,根据题意画出图形,在解答(3)时要注意进行分类讨论.

| A. | $\frac{\sqrt{3}}{3}$,60° | B. | 1,45° | C. | $\sqrt{3}$,60° | D. | $\frac{\sqrt{3}}{3}$,30° |
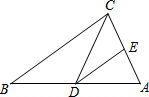 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,且∠DCE=∠B.那么下列各判断中,错误的是( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,且∠DCE=∠B.那么下列各判断中,错误的是( )| A. | △ADE∽△ABC | B. | △ADE∽△ACD | C. | △DEC∽△CDB | D. | △ADE∽△DCB |
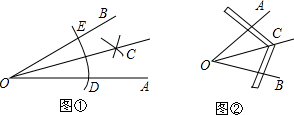
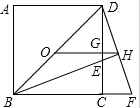 已知:如图,正方形ABCD中,O是BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG.
已知:如图,正方形ABCD中,O是BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG.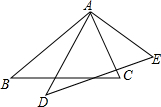 如图,已知△ABC≌△ADE,D是∠BAC的平分线上一点,且∠BAC=70°,则∠CAE=35度.
如图,已知△ABC≌△ADE,D是∠BAC的平分线上一点,且∠BAC=70°,则∠CAE=35度. 已知二次函数y=2x2-4x-6.
已知二次函数y=2x2-4x-6. 如图,在梯形ABCD中,AD∥BC,AB=DC,BC=AC,∠ACD=30°,则∠D=110°.
如图,在梯形ABCD中,AD∥BC,AB=DC,BC=AC,∠ACD=30°,则∠D=110°.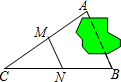 A、B两点被池塘隔开(如图),在AB外选一点C,连结AC和BC并分别找出其中点M、N,若测得MN=100m,则A、B两点的距离为200m.
A、B两点被池塘隔开(如图),在AB外选一点C,连结AC和BC并分别找出其中点M、N,若测得MN=100m,则A、B两点的距离为200m.