题目内容
8.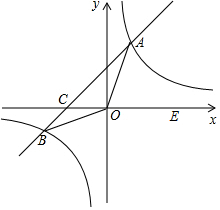 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{12}{x}$的图象交于A、B两点,与x轴交于点C;点A在第一象限,点B的坐标为(-6,n);E为x轴正半轴上一点,且tan∠AOE=$\frac{4}{3}$.
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{12}{x}$的图象交于A、B两点,与x轴交于点C;点A在第一象限,点B的坐标为(-6,n);E为x轴正半轴上一点,且tan∠AOE=$\frac{4}{3}$.(1)求点A的坐标;
(2)求一次函数的表达式;
(3)求△AOB的面积.
分析 (1)过A作AH⊥x轴于点H,根据tan∠AOE=$\frac{AH}{OH}$=$\frac{4}{3}$,设OH=3k,AH=4k,即A的坐标为(3k,4k),代入反比例函数解析式即可求出A点的坐标;
(2)求出B点的坐标,把A、B的坐标代入y=kx+b即可求出k、b的值,即可求出答案;
(3)求出OC,根据三角形面积公式求出即可.
解答 解:(1)过A作AH⊥x轴于点H,
在Rt△AOH中,∵tan∠AOE=$\frac{AH}{OH}$=$\frac{4}{3}$,
∴设OH=3k,AH=4k,
即A的坐标为(3k,4k),其中k>0,
∵A在y=$\frac{12}{x}$图象上,
∴4k=$\frac{12}{3k}$,
解得:k=1(负数舍去),
∴A的坐标为(3,4);
(2)∵点B(-6,n)在y=$\frac{12}{x}$的图象上,
∴代入得:n=-2,
即B的坐标为(-6,-2),
把A、B的坐标代入y=kx+b(k≠0)得:$\left\{\begin{array}{l}{3k+b=4}\\{-6k+b=-2}\end{array}\right.$,
解得:k=$\frac{2}{3}$,b=2,
∴一次函数的表达式是y=$\frac{2}{3}$x+2;
(3)在y=$\frac{2}{3}$x+2中令y=0,则x=-3,
即C(-3,0),
所以S△AOB=S△AOC+S△BOC=$\frac{1}{2}$×|-3|×4+$\frac{1}{2}$×|-3|×|-2|=9,
即△AOB的面积是9.
点评 本题考查了反比例函数与一次函数的交点问题,用待定系数法求出一次函数的解析式等知识点,能用待定系数法求出一次函数的解析式是解此题的关键.

练习册系列答案
相关题目
19.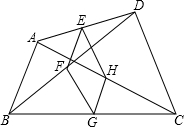 如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )
如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )
 如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )
如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )| A. | AB∥DC | B. | AC=BD | C. | AC⊥BD | D. | AB=DC |
20.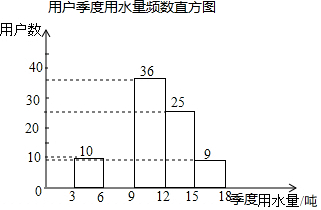 某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:
某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:
用户季度用水量频数分布表
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=20,n=0.25;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本季度水量定为每户每季度9吨,不超过基本季度用水量的部分享受基本价格,超出基本季度用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
 某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:
某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:用户季度用水量频数分布表
| 平均用水量(吨) | 频数 | 频率 |
| 3<x≤6 | 10 | 0.1 |
| 6<x≤9 | m | 0.2 |
| 9<x≤12 | 36 | 0.36 |
| 12<x≤15 | 25 | n |
| 15<x≤18 | 9 | 0.09 |
(1)在频数分布表中:m=20,n=0.25;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本季度水量定为每户每季度9吨,不超过基本季度用水量的部分享受基本价格,超出基本季度用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
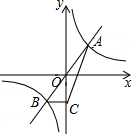 如图,已知函数y=kx 与函数y=$\frac{k}{x}$的图象交于A、B 两点,过点B作BC⊥y 轴,垂足为C,连接AC.若△ABC 的面积为2,则k 的值为2.
如图,已知函数y=kx 与函数y=$\frac{k}{x}$的图象交于A、B 两点,过点B作BC⊥y 轴,垂足为C,连接AC.若△ABC 的面积为2,则k 的值为2. 请仅用无刻度的直尺,作出下列各图中∠AOB的平分线,保留作图痕迹.
请仅用无刻度的直尺,作出下列各图中∠AOB的平分线,保留作图痕迹. 如图,?ABCD的对角线AC,BD相交于点O,且AB=5,AC=8,BD=6,求证:?ABCD是菱形.
如图,?ABCD的对角线AC,BD相交于点O,且AB=5,AC=8,BD=6,求证:?ABCD是菱形. 如图,在四边形ABCD中,已知AB∥DC,AB=DC,在不添加任何辅助线的情况下,请补充一个条件,使四边形ABCD成为矩形,这个条件是∠A=90°.
如图,在四边形ABCD中,已知AB∥DC,AB=DC,在不添加任何辅助线的情况下,请补充一个条件,使四边形ABCD成为矩形,这个条件是∠A=90°. 如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,正确结论的个数为( )
如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,正确结论的个数为( )