题目内容
19.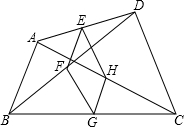 如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )
如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )| A. | AB∥DC | B. | AC=BD | C. | AC⊥BD | D. | AB=DC |
分析 由点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,根据三角形中位线的性质,可得EF=GH=$\frac{1}{2}$AB,EH=FG=$\frac{1}{2}$CD,又由当EF=FG=GH=EH时,四边形EFGH是菱形,即可求得答案.
解答 解:∵点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,
∴EF=GH=$\frac{1}{2}$AB,EH=FG=$\frac{1}{2}$CD,
∵当EF=FG=GH=EH时,四边形EFGH是菱形,
∴当AB=CD时,四边形EFGH是菱形.
故选:D.
点评 此题考查了中点四边形的性质、菱形的判定以及三角形中位线的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
7.通讯员要在规定时间内到达某地,他每小时走15千米,则可提前24分钟到达某地;如果每小时走12千米,则要迟到15分钟.设通讯员到达某地的路程是x千米,原定的时间为y小时,则可列方程组为( )
| A. | $\left\{\begin{array}{l}{\frac{x}{15}-15=y}\\{\frac{x}{12}+12=y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\frac{x}{15}+15=y}\\{\frac{x}{12}-12=y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{x}{15}-\frac{24}{60}=y}\\{\frac{x}{12}-\frac{15}{60}=y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x}{15}+\frac{24}{60}=y}\\{\frac{x}{12}-\frac{15}{60}=y}\end{array}\right.$ |
4. 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB、EC、DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB、EC、DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB、EC、DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB、EC、DB,添加一个条件,不能使四边形DBCE成为矩形的是( )| A. | AB=BE | B. | BE⊥DC | C. | ∠ADB=90° | D. | CE⊥DE |
 如图,⊙M经过原点O和点A(4,0)、点B(0,3),点P是⊙M上一点,并在x轴上方,则sin∠P=$\frac{4}{5}$.
如图,⊙M经过原点O和点A(4,0)、点B(0,3),点P是⊙M上一点,并在x轴上方,则sin∠P=$\frac{4}{5}$.
 如图,某学员在广场上练习驾驶汽车,第一次向左拐弯15度行驶一段后,第二次向左拐弯13度,再次行驶一段后,那么第三次要向右拐弯28度,则行驶方向与原来行驶方向相同.
如图,某学员在广场上练习驾驶汽车,第一次向左拐弯15度行驶一段后,第二次向左拐弯13度,再次行驶一段后,那么第三次要向右拐弯28度,则行驶方向与原来行驶方向相同.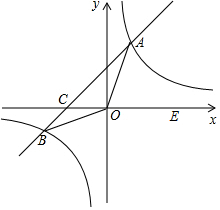 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{12}{x}$的图象交于A、B两点,与x轴交于点C;点A在第一象限,点B的坐标为(-6,n);E为x轴正半轴上一点,且tan∠AOE=$\frac{4}{3}$.
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{12}{x}$的图象交于A、B两点,与x轴交于点C;点A在第一象限,点B的坐标为(-6,n);E为x轴正半轴上一点,且tan∠AOE=$\frac{4}{3}$.