题目内容
5.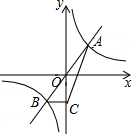 如图,已知函数y=kx 与函数y=$\frac{k}{x}$的图象交于A、B 两点,过点B作BC⊥y 轴,垂足为C,连接AC.若△ABC 的面积为2,则k 的值为2.
如图,已知函数y=kx 与函数y=$\frac{k}{x}$的图象交于A、B 两点,过点B作BC⊥y 轴,垂足为C,连接AC.若△ABC 的面积为2,则k 的值为2.
分析 根据正比例函数y=kx(k>0)与反比例函数y=$\frac{k}{x}$的图象均关于原点对称,可表示出A、B、C点坐标,再根据三角形的面积公式即可得到关于k的方程,解方程即可.
解答 解:∵正比例函数y=kx(k>0)与反比例函数y=$\frac{k}{x}$的图象均关于原点对称,
∴设A点坐标为(x,$\frac{k}{x}$),则B(-x,-$\frac{k}{x}$),C(0,-$\frac{k}{x}$),
∴S△COB=$\frac{1}{2}$OC•BC=$\frac{1}{2}$|-x|•$\frac{k}{x}$=$\frac{k}{2}$,
S△AOC=$\frac{1}{2}$OC•|x|=$\frac{1}{2}$|-$\frac{k}{x}$|•x=$\frac{k}{2}$,
∴S△ABC=S△AOB+S△BOC=$\frac{k}{2}$+$\frac{k}{2}$=2,
∴k=2.
故答案为2.
点评 本题考查的是反比例函数与正比例函数图象的特点,解答此题的关键是表示出A、B、C点坐标.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
7.通讯员要在规定时间内到达某地,他每小时走15千米,则可提前24分钟到达某地;如果每小时走12千米,则要迟到15分钟.设通讯员到达某地的路程是x千米,原定的时间为y小时,则可列方程组为( )
| A. | $\left\{\begin{array}{l}{\frac{x}{15}-15=y}\\{\frac{x}{12}+12=y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\frac{x}{15}+15=y}\\{\frac{x}{12}-12=y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{x}{15}-\frac{24}{60}=y}\\{\frac{x}{12}-\frac{15}{60}=y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x}{15}+\frac{24}{60}=y}\\{\frac{x}{12}-\frac{15}{60}=y}\end{array}\right.$ |

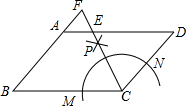 如图,在?ABCD中,AB=6,BC=8,以C为圆心适当长为半径画弧分别交BC,CD于M,N两点,分别以M,N为圆心,以大于$\frac{1}{2}$MN的长为半径画弧,两弧在∠BCD的内部交于点P,连接CP并延长交AD于E,交BA的延长线于F,则AE+AF的值等于4.
如图,在?ABCD中,AB=6,BC=8,以C为圆心适当长为半径画弧分别交BC,CD于M,N两点,分别以M,N为圆心,以大于$\frac{1}{2}$MN的长为半径画弧,两弧在∠BCD的内部交于点P,连接CP并延长交AD于E,交BA的延长线于F,则AE+AF的值等于4.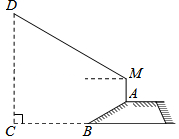 如图,防洪大堤的横截面是梯形,背水坡AB的坡度i=1:$\sqrt{3}$,AB=20米,身高为1.7米的小明站在大堤A点,测得高压电线杆的顶端D的仰角为30°,已知地而BC宽30米.
如图,防洪大堤的横截面是梯形,背水坡AB的坡度i=1:$\sqrt{3}$,AB=20米,身高为1.7米的小明站在大堤A点,测得高压电线杆的顶端D的仰角为30°,已知地而BC宽30米. 如图,△ABC中,AB=AC,AD、AE分别是∠BAC和外角∠BAF的平分线,且BE⊥AE.
如图,△ABC中,AB=AC,AD、AE分别是∠BAC和外角∠BAF的平分线,且BE⊥AE. 如图,⊙M经过原点O和点A(4,0)、点B(0,3),点P是⊙M上一点,并在x轴上方,则sin∠P=$\frac{4}{5}$.
如图,⊙M经过原点O和点A(4,0)、点B(0,3),点P是⊙M上一点,并在x轴上方,则sin∠P=$\frac{4}{5}$.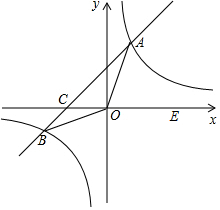 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{12}{x}$的图象交于A、B两点,与x轴交于点C;点A在第一象限,点B的坐标为(-6,n);E为x轴正半轴上一点,且tan∠AOE=$\frac{4}{3}$.
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{12}{x}$的图象交于A、B两点,与x轴交于点C;点A在第一象限,点B的坐标为(-6,n);E为x轴正半轴上一点,且tan∠AOE=$\frac{4}{3}$.