题目内容
13．化简$\frac{{3{m^2}}}{9mn}$=$\frac{m}{3n}$．分析 首先确定分子与分母的公因式，系数是分子与分母的系数的最大公约数，相同的字母，取最小的次数作为公因式的字母的次数，确定公因式以后，把公因式约去即可．
解答 解：$\frac{{3{m^2}}}{9mn}$=$\frac{m}{3n}$，
故答案为：$\frac{m}{3n}$
点评 本题考查了约分，约分的依据是分时的基本性质，确定公因式是关键．
练习册系列答案
阅读快车系列答案
相关题目
3．已知2-$\sqrt{3}$是关于x的方程x2-4x+c=0的一个根，则方程的另一个根与c的值是（ ）
| A． | $\sqrt{3}$-2，-1 | B． | -6-$\sqrt{3}$，15-8$\sqrt{3}$ | C． | 2+$\sqrt{3}$，1 | D． | 2+$\sqrt{3}$，7-4$\sqrt{3}$ |
如图，已知AD⊥EF，CE⊥EF，∠2+∠3=180°．
8．下列等式一定成立的是（ ）
| A． | $\sqrt{9}$-$\sqrt{4}$=$\sqrt{5}$ | B． | |1-$\sqrt{3}$|=$\sqrt{3}$-1 | C． | $\sqrt{9}$=±3 | D． | -$\sqrt{（-9）^{2}}$=9 |
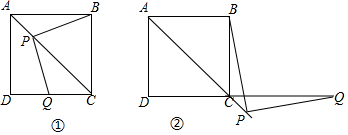
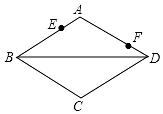如图，周长为16的菱形ABCD中，点E，F分别在AB，AD边上，AE=1，AF=3，P为BD上一动点，则线段EP+FP的长最短为4．
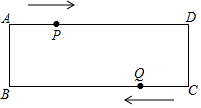如图，在矩形ABCD中，AB=4cm，AD=12cm，点P在AD边上以每秒1cm的速度从点A向点D运动，点Q在BC边上，以每秒4cm的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时停止（同时点Q也停止），在这段时间内，线段PQ有（ ）次平行于AB？