题目内容
8.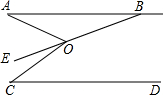 如图,已知,AB∥CD,B是∠AOC的角平分线OE的反向延长线与直线AB的交点,若∠A+∠C=90°,∠ABE=15°,则∠C=60°.
如图,已知,AB∥CD,B是∠AOC的角平分线OE的反向延长线与直线AB的交点,若∠A+∠C=90°,∠ABE=15°,则∠C=60°.
分析 延长AO交CD于M,根据平行线的性质得出∠A=∠AMC,求出∠AOC=∠C+∠AMC=90°,根据角平分线定义求出∠AOE=45°,根据三角形外角性质求出∠A即可.
解答 解: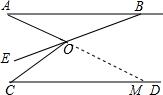
延长AO交CD于M,
∵AB∥CD,
∴∠A=∠AMC,
∵∠A+∠C=90°,
∴∠C+∠AMC=90°,
∴∠AOC=∠C+∠AMC=90°,
∵OE平分∠AOC,
∴∠AOE=$\frac{1}{2}$×90°=45°,
∵∠ABE=15°,
∴∠A=∠AOE-∠ABE=30°,
∴∠C=90°-30°=60°,
故答案为:60
点评 本题考查了平行线的性质,三角形外角性质的应用,解此题的关键是求出∠AOE和∠A的度数,题目比较好,难度适中.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
18.已知a方程2x2+3x-4=0的一个根,则代数式2a2+3a的值等于( )
| A. | 4 | B. | 0 | C. | 1 | D. | 2 |
16.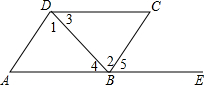 如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
 如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠A=∠5 | D. | ∠A+∠ABC=180° |
13.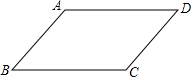 如图,下面推理中,正确的是( )
如图,下面推理中,正确的是( )
 如图,下面推理中,正确的是( )
如图,下面推理中,正确的是( )| A. | ∵∠A+∠D=180°∴AD∥BC | B. | ∵∠C+∠D=180°∴AB∥CD | ||
| C. | ∵∠A+∠D=180°∴AB∥CD | D. | ∵∠B+∠C=180°∴AD∥BC |
17.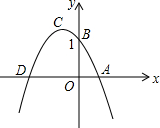 如图是二次函数y=mx2+nx+b的图象,已知它的顶点C在第二象限,且经过点A(1,0),点B(0,1),与x轴另一交点为D,当△ACD的面积为△ABD面积的$\frac{3}{2}$倍时,m的值为( )
如图是二次函数y=mx2+nx+b的图象,已知它的顶点C在第二象限,且经过点A(1,0),点B(0,1),与x轴另一交点为D,当△ACD的面积为△ABD面积的$\frac{3}{2}$倍时,m的值为( )
 如图是二次函数y=mx2+nx+b的图象,已知它的顶点C在第二象限,且经过点A(1,0),点B(0,1),与x轴另一交点为D,当△ACD的面积为△ABD面积的$\frac{3}{2}$倍时,m的值为( )
如图是二次函数y=mx2+nx+b的图象,已知它的顶点C在第二象限,且经过点A(1,0),点B(0,1),与x轴另一交点为D,当△ACD的面积为△ABD面积的$\frac{3}{2}$倍时,m的值为( )| A. | $\sqrt{3}$-2 | B. | -2±$\sqrt{3}$ | C. | 2-$\sqrt{3}$ | D. | -2-$\sqrt{3}$ |