题目内容
3.解方程(1)(x+3)2=2
(2)x2+2x-5=0
(3)(x-3)(x+7)=-9
(4)3x2=6x-2.
分析 (1)利用直接开平方法解方程;
(2)利用配方法解方程;
(3)先把方程化为一般式,然后利用因式分解法解方程;
(4)先把方程化为一般式,然后利用公式法解方程.
解答 解:(1)x+3=±$\sqrt{2}$,
所以x1=-3+$\sqrt{2}$,x2=-3-$\sqrt{2}$;
(2)x2+2x+1=6,
(x+1)2=6,
x+1=±$\sqrt{6}$,
所以x1=-1+$\sqrt{6}$,x2=-1-$\sqrt{6}$;
(2)x2+4x-12=0,
(x+6)(x-2)=0,
x+6=0或x-2=0,
所以x1=-6,x2=2;
(3)3x2-6x+2=0,
△=(-6)2-4×3×2=12,
x=$\frac{6±\sqrt{12}}{2×3}$=$\frac{3±\sqrt{3}}{3}$,
所以x1=$\frac{3+\sqrt{3}}{3}$,x2=$\frac{3-\sqrt{3}}{3}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了直接开平方法和公式法解一元二次方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.二元一次方程4x+3y=25的自然数解有( )
| A. | 2组 | B. | 3组 | C. | 4组 | D. | 5组 |
15.等腰三角形的两边长分别是4和5,则这个等腰三角形的周长是( )
| A. | 13或14 | B. | 13 | C. | 14 | D. | 无法确定 |
12.在实数0,-$\sqrt{2}$,-$\frac{2}{3}$,|-1|中,最小的数是( )
| A. | -$\frac{2}{3}$ | B. | -$\sqrt{2}$ | C. | 0 | D. | |-1| |
 如图,直线l上有三个正方形a,b,c,若a,c的面积分别为4和10,则b的面积为14.
如图,直线l上有三个正方形a,b,c,若a,c的面积分别为4和10,则b的面积为14. 如图所示:∠1=30°,直线AB与CD相交于点O,已知,OE是∠BOC的平分线,则∠2=30°,∠3=75°.
如图所示:∠1=30°,直线AB与CD相交于点O,已知,OE是∠BOC的平分线,则∠2=30°,∠3=75°.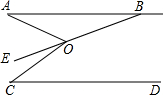 如图,已知,AB∥CD,B是∠AOC的角平分线OE的反向延长线与直线AB的交点,若∠A+∠C=90°,∠ABE=15°,则∠C=60°.
如图,已知,AB∥CD,B是∠AOC的角平分线OE的反向延长线与直线AB的交点,若∠A+∠C=90°,∠ABE=15°,则∠C=60°.