题目内容
17.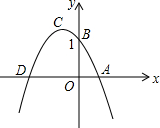 如图是二次函数y=mx2+nx+b的图象,已知它的顶点C在第二象限,且经过点A(1,0),点B(0,1),与x轴另一交点为D,当△ACD的面积为△ABD面积的$\frac{3}{2}$倍时,m的值为( )
如图是二次函数y=mx2+nx+b的图象,已知它的顶点C在第二象限,且经过点A(1,0),点B(0,1),与x轴另一交点为D,当△ACD的面积为△ABD面积的$\frac{3}{2}$倍时,m的值为( )| A. | $\sqrt{3}$-2 | B. | -2±$\sqrt{3}$ | C. | 2-$\sqrt{3}$ | D. | -2-$\sqrt{3}$ |
分析 首先把A(1,0),B(0,l)代入y=mx2+nx+b,求出m和n的关系式,然后求出顶点C的纵坐标,根据△ACD的面积为△ABD面积的$\frac{3}{2}$倍,列出m的一元二次方程,结合题意求出m的值即可.
解答 解:将A(1,0),B(0,l)代入y=mx2+nx+b,
得:$\left\{\begin{array}{l}{m+n+b=0}\\{b=1}\end{array}\right.$,
可得:m+n=-1,
则函数的解析式得到:y=mx2-(m+1)x+1,
顶点C的纵坐标为$\frac{4m-(m+1)^{2}}{4m}$,
因为△ACD的面积为△ABD面积的$\frac{3}{2}$倍,
由同底可知:$\frac{4m-(m+1)^{2}}{4m}$=$\frac{3}{2}$,
整理得:m2+4m+1=0,
解得:m=-2$±\sqrt{3}$,
由图象可知:a<0,
∵抛物线过点(1,0),顶点M在第二象限,其对称轴x=$\frac{m+1}{2m}$,
∴-1<m<0,
∴m=-2-$\sqrt{3}$舍去,
∴m=-2+$\sqrt{3}$,
故选A.
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键是求出m和n的关系以及求出顶点C的坐标,此题难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.在实数0,-$\sqrt{2}$,-$\frac{2}{3}$,|-1|中,最小的数是( )
| A. | -$\frac{2}{3}$ | B. | -$\sqrt{2}$ | C. | 0 | D. | |-1| |
2.-|-a|是一个( )
| A. | 正数 | B. | 正数或零 | C. | 负数 | D. | 负数或零 |
6.顺次连接对角线互相垂直的四边形的中点的四边形是( )
| A. | 矩形 | B. | 直角梯形 | C. | 菱形 | D. | 正方形 |
 如图,点P是?ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:
如图,点P是?ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论: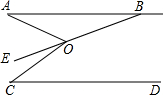 如图,已知,AB∥CD,B是∠AOC的角平分线OE的反向延长线与直线AB的交点,若∠A+∠C=90°,∠ABE=15°,则∠C=60°.
如图,已知,AB∥CD,B是∠AOC的角平分线OE的反向延长线与直线AB的交点,若∠A+∠C=90°,∠ABE=15°,则∠C=60°.
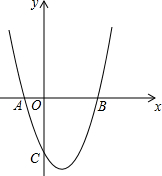 如图,在平面直角坐标系中,点O是坐标原点,抛物线y=x2+bx+c与直线y=2x-6交于x轴正半轴上的B点,抛物线与x轴的负半轴交于点A,与y轴的负半轴交于点C,OB=3OA.
如图,在平面直角坐标系中,点O是坐标原点,抛物线y=x2+bx+c与直线y=2x-6交于x轴正半轴上的B点,抛物线与x轴的负半轴交于点A,与y轴的负半轴交于点C,OB=3OA.