题目内容
1. 如图,∠CDE+∠CED=90°,EM平分∠CED,并与CD边交于点M.DN平分∠CED,并与EM交于点N.
如图,∠CDE+∠CED=90°,EM平分∠CED,并与CD边交于点M.DN平分∠CED,并与EM交于点N.(1)依题意补全图形,并猜想∠EDN+∠NED的度数等于45°;
(2)证明以上结论.
证明:∵DN平分∠CDE,EM平分∠CED,
∴∠EDN=$\frac{1}{2}∠CDE$,∠NED=$\frac{1}{2}∠$CED.(理由:角平分线的定义)
∵∠CDE+∠CED=90°,
∴∠EDN+∠NED=$\frac{1}{2}$×(∠CDE+∠CED)=$\frac{1}{2}$×90°=45°.
分析 (1)根据题意画出图形,然后由角平分线的定义可求得∠EDN+∠NED=45°;
(2)根据角平分线的定义以及证明过程进行填写即可.
解答 (1)解:如图所示:
猜想∠EDN+∠NED=45°.
(2)证明:∵DN平分∠CDE,EM平分∠CED,
∴∠EDN=$\frac{1}{2}∠CDE$,∠NED=$\frac{1}{2}∠$CED.(理由:角平分线的定义),
∵∠CDE+∠CED=90°,
∴∠EDN+∠NED=$\frac{1}{2}$(∠CDE+∠CED)=$\frac{1}{2}×90°$=45°.
故答案为:(1)45°;(2)$\frac{1}{2}∠$CED;角平分线的定义;$\frac{1}{2}$;CDE;CED;$\frac{1}{2}$;45.
点评 本题主要考查的是角的计算、角平分线的定义,逆用乘法的分配律求得∠EDN+∠NED=$\frac{1}{2}$(∠CDE+∠CED)是解题的关键.

练习册系列答案
相关题目
11.聪聪的文件夹里放了大小相同的试卷共12页,其中语文6页,数学4页,英语2页,他随机地从讲义夹中抽出1页,抽出的试卷恰好是数学试卷的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
6. 如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )
如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )
 如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )
如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )| A. | 0<x<1 | B. | -1<x<0 | C. | x<0或x>1 | D. | x<-1或x>0 |
 如图,点D、E分别是AB、AC上的点,将△ABC沿着DE对折,A点落在BC边的F点上,若∠B=50°,∠C=70°,则∠BDF+∠CEF=120°.
如图,点D、E分别是AB、AC上的点,将△ABC沿着DE对折,A点落在BC边的F点上,若∠B=50°,∠C=70°,则∠BDF+∠CEF=120°. 如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),且点A的坐标是(-1,0),与y轴交于点C,点C的坐标是(0,3),连接AC.
如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),且点A的坐标是(-1,0),与y轴交于点C,点C的坐标是(0,3),连接AC.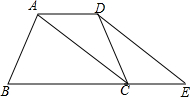 如图,在梯形ABCD中,AD∥BC,CA平分∠BCD,将△ADC绕DC的中点旋转180°到△ECD处,B、C、E三点在同一直线上,∠B=2∠E.
如图,在梯形ABCD中,AD∥BC,CA平分∠BCD,将△ADC绕DC的中点旋转180°到△ECD处,B、C、E三点在同一直线上,∠B=2∠E. 如图,已知△ABC,点D在边BC上,点E在边AC上,点F在边AB上,且DE∥D1E1,EF∥E1F1,DF∥D1F1.求证:S△DEF•S△D1E1F1=S2△ABC.
如图,已知△ABC,点D在边BC上,点E在边AC上,点F在边AB上,且DE∥D1E1,EF∥E1F1,DF∥D1F1.求证:S△DEF•S△D1E1F1=S2△ABC.