题目内容
15.明明利用自制“四旋翼”无人机进行数学研究活动,无人机传递数据显示,无人机A与地面CD的距离为420米,从无人机底部A处看“河南大玉米”(郑州会展中心千禧大夏)顶部B的俯角为30°,看这栋大楼底部C的俯角为60°,求“河南大玉米”的高度.($\sqrt{2}≈1.414,\sqrt{3}≈1.732,\sqrt{5}$≈2.236,结果精确到1m.)
分析 根据题意,作辅助线BE⊥AD于点E,构造出直角三角形,由题目中的信息可以得到DE的长,BC=DE,从而得到BC的长,本题得以解决.
解答 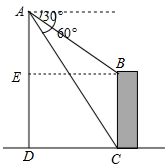 解:作BE⊥AD于点E,如右图所示,
解:作BE⊥AD于点E,如右图所示,
由已知可得,
∠ACD=60°,∠AEB=∠ADC=90°,∠ABE=30°,AD=420米,
∴BE=$\frac{AE}{sin30°}$,CD=$\frac{AD}{sin60°}$,
∵BE=CD,
∴$\frac{AE}{sin30°}=\frac{AD}{sin60°}$,
即$\frac{AE}{\frac{1}{2}}=\frac{420}{\frac{\sqrt{3}}{2}}$,
解得,AE=140$\sqrt{3}$,
∴DE=AD-AE=420-140$\sqrt{3}$≈178米,
∵BC=DE,
∴BC=178米,
即“河南大玉米”的高度约为178米.
点评 本题考查解直角三角形的应用-仰角俯角问题,解题的关键是明确题意,构造合适的直角三角形,利用数形结合的思想解答,注意最后结果要精确到1m.

练习册系列答案
相关题目
10. 如图,那么|a-b|+$\sqrt{(a+b)^{2}}$的结果是( )
如图,那么|a-b|+$\sqrt{(a+b)^{2}}$的结果是( )
 如图,那么|a-b|+$\sqrt{(a+b)^{2}}$的结果是( )
如图,那么|a-b|+$\sqrt{(a+b)^{2}}$的结果是( )| A. | -2b | B. | 2b | C. | -2a | D. | 2a |
7.在实数-2$\sqrt{5}$、0、-5、3中,最小的实数是( )
| A. | -2$\sqrt{5}$ | B. | 0 | C. | -5 | D. | 3 |
5.已知:(a-b)2=9;(a+b)2=25,则a2+b2=( )
| A. | 34 | B. | 16 | C. | -16 | D. | 17 |
 将一组整数按如图所示的规律排列下去,若有序数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示的数为8,则(7,4)表示的数是( )
将一组整数按如图所示的规律排列下去,若有序数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示的数为8,则(7,4)表示的数是( )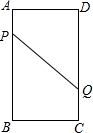 A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别从A、C同时出发,点P以3厘米每秒的速度向点B移动,一直到达点B为止,点Q以2厘米每秒的速度向点D移动.
A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别从A、C同时出发,点P以3厘米每秒的速度向点B移动,一直到达点B为止,点Q以2厘米每秒的速度向点D移动.