题目内容
13. 已知:当x>0时,反比例函数y1=$\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A、B.
已知:当x>0时,反比例函数y1=$\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A、B.(1)若A点的坐标为(2,a),求a、b的值;
(2)在(1)的条件下,连接OA、OB,求△OAB的面积;
(3)结合图象,写出在第一、四象限内,y1>y3>y2时,x的取值范围.
分析 (1)把A(2,a)代入y1=$\frac{4}{x}$即可求得a,然后代入直线y3=-x+b即可求得b;
(2)根据直线的解析式求得直线与x轴的交点坐标,然后根据S△OAB=S△AOC+S△BOC即可求得;
(3)根据图象即可求得.
解答 解:(1)∵点A是反比例函数y1=$\frac{4}{x}$图象上的点,
∴a=$\frac{4}{2}$=2,
∴A(2,2),
∵点A在直线y3=-x+b上,
∴2=-2+b,
∴b=4.
(2)设直线与x轴的交点为C,
由直线y3=-x+4可知直线与x轴的交点坐标为C(4,0),
解$\left\{\begin{array}{l}{y=-x+4}\\{y=-\frac{5}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=5}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=5}\\{{y}_{2}=-1}\end{array}\right.$,
∴B(5,-1),
∴S△OAB=S△AOC+S△BOC=$\frac{1}{2}$×4×2+$\frac{1}{2}$×4×1=6;
(3)由图象可知:y1>y3>y2时x的取值范围为0<x<5且x≠2.
点评 本题考查了反比例函数和一次函数的交点问题,待定系数法求一次函数的解析式以及函数图象上点的坐标特征;数形结合思想的运用是本题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
3.满足下列条件的△ABC不是直角三角形的是( )
| A. | a=1、b=2,c=$\sqrt{3}$ | B. | a=1、b=2,c=$\sqrt{5}$ | C. | a:b:c=3:4:5 | D. | ∠A:∠B:∠C=3:4:5 |
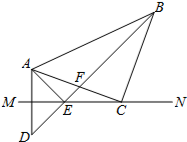 如图,已知,MN是AD的垂直平分线,点C在MN上,∠MCA=20°,∠ACB=90°,CA=CB=5,BD交MN于点E,交AC于点F,连接AE.
如图,已知,MN是AD的垂直平分线,点C在MN上,∠MCA=20°,∠ACB=90°,CA=CB=5,BD交MN于点E,交AC于点F,连接AE.  如图,是一块四边形绿地的示意图,其中AB长为24米,BC长15米,CD长为20米,DA长7米,∠C=90°,求绿地ABCD的面积.
如图,是一块四边形绿地的示意图,其中AB长为24米,BC长15米,CD长为20米,DA长7米,∠C=90°,求绿地ABCD的面积. 如图,一次函数y1=kx+b和反比例函数y2=$\frac{m}{x}$的图象交于A、B两点.
如图,一次函数y1=kx+b和反比例函数y2=$\frac{m}{x}$的图象交于A、B两点. 如图,∠AOB=35°,∠BOC=90°,OD是∠AOC的平分线.求∠BOD的度数.
如图,∠AOB=35°,∠BOC=90°,OD是∠AOC的平分线.求∠BOD的度数.