题目内容
1. 如图,是一块四边形绿地的示意图,其中AB长为24米,BC长15米,CD长为20米,DA长7米,∠C=90°,求绿地ABCD的面积.
如图,是一块四边形绿地的示意图,其中AB长为24米,BC长15米,CD长为20米,DA长7米,∠C=90°,求绿地ABCD的面积.
分析 连接BD,先根据勾股定理求出BD的长,再由勾股定理的逆定理判定△ABD为直角三角形,则四边形ABCD的面积=直角△BCD的面积+直角△ABD的面积.
解答 解:连接BD.如图所示:
∵∠C=90°,BC=15米,CD=20米,
∴BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{1{5}^{2}+2{0}^{2}}$=25(米);
在△ABD中,∵BD=25米,AB=24米,DA=7米,
242+72=252,即AB2+BD2=AD2,
∴△ABD是直角三角形.
∴S四边形ABCD=S△ABD+S△BCD
=$\frac{1}{2}$AB•AD+$\frac{1}{2}$BC•CD
=$\frac{1}{2}$×24×7+$\frac{1}{2}$×15×20
=84+150
=234(平方米);
即绿地ABCD的面积为234平方米.
点评 本题考查勾股定理及其逆定理的应用.解答此题的关键是作出辅助线,构造出直角三角形,求出BD的长.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
6.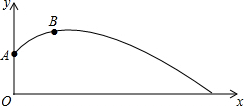 小明为了检测自己实心球的训练情况,再一次投掷的测试中,实心球经过的抛物线如图所示,其中出手点A的坐标为(0,$\frac{16}{9}$),球在最高点B的坐标为(3,$\frac{25}{9}$).
小明为了检测自己实心球的训练情况,再一次投掷的测试中,实心球经过的抛物线如图所示,其中出手点A的坐标为(0,$\frac{16}{9}$),球在最高点B的坐标为(3,$\frac{25}{9}$).
(1)求抛物线的解析式;
(2)已知某市男子实心球的得分标准如表:
假设小明是春谷中学九年级的男生,求小明在实心球训练中的得分;
(3)在小明练习实心球的正前方距离投掷点7米处有一个身高1.2米的小朋友在玩耍,问该小朋友是否有危险(如果实心球在小孩头顶上方飞出为安全,否则视为危险),请说明理由.
 小明为了检测自己实心球的训练情况,再一次投掷的测试中,实心球经过的抛物线如图所示,其中出手点A的坐标为(0,$\frac{16}{9}$),球在最高点B的坐标为(3,$\frac{25}{9}$).
小明为了检测自己实心球的训练情况,再一次投掷的测试中,实心球经过的抛物线如图所示,其中出手点A的坐标为(0,$\frac{16}{9}$),球在最高点B的坐标为(3,$\frac{25}{9}$).(1)求抛物线的解析式;
(2)已知某市男子实心球的得分标准如表:
| 得分 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| 掷远(米) | 8.6 | 8.3 | 8 | 7.7 | 7.3 | 6.9 | 6.5 | 6.1 | 5.8 | 5.5 | 5.2 | 4.8 | 4.4 | 4.0 | 3.5 | 3.0 |
(3)在小明练习实心球的正前方距离投掷点7米处有一个身高1.2米的小朋友在玩耍,问该小朋友是否有危险(如果实心球在小孩头顶上方飞出为安全,否则视为危险),请说明理由.

 已知,如图,点A、B、C、D在一条直线上,AB=CD,EA∥FB,EC∥FD,求证:EA=FB.
已知,如图,点A、B、C、D在一条直线上,AB=CD,EA∥FB,EC∥FD,求证:EA=FB. 如图,在4×4的正方形网格中,每小正方形的边长均为1,△ABC的顶点A、B、C均在格点上.
如图,在4×4的正方形网格中,每小正方形的边长均为1,△ABC的顶点A、B、C均在格点上. 在平面直角坐标系中,△ABC的点坐标分别是A(2,4)、B(1,2)、C(5,3),如图:
在平面直角坐标系中,△ABC的点坐标分别是A(2,4)、B(1,2)、C(5,3),如图: 已知:当x>0时,反比例函数y1=$\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A、B.
已知:当x>0时,反比例函数y1=$\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A、B. 如图,AB是⊙O直径,直径AB⊥弦CD于点E,四边形ADCF是平行四边形,CD=4$\sqrt{3}$,BE=2.
如图,AB是⊙O直径,直径AB⊥弦CD于点E,四边形ADCF是平行四边形,CD=4$\sqrt{3}$,BE=2.