题目内容
4.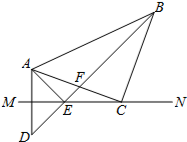 如图,已知,MN是AD的垂直平分线,点C在MN上,∠MCA=20°,∠ACB=90°,CA=CB=5,BD交MN于点E,交AC于点F,连接AE.
如图,已知,MN是AD的垂直平分线,点C在MN上,∠MCA=20°,∠ACB=90°,CA=CB=5,BD交MN于点E,交AC于点F,连接AE. (1)求∠CBE,∠CAE的度数;
(2)求AE2+BE2的值.
分析 (1)连接CD,利用轴对称的性质进行解答即可;
(2)根据勾股定理进行解答即可.
解答 解:(1)连接CD,
∵MN垂直平分AD,点C,E在MN上,
∴根据点A,D关于MN的对称性,得 CA=CD,∠MCD=∠MCA,∠CAE=∠CDE,
∵CA=CB,
∴CB=CD,
∴∠CBE=∠CDB,
∴∠CBE=∠CAE,
∵∠MCA=20°,
∴∠MCD=20°,
∵∠ACB=90°,
∴∠BCD=130°,
∴∠CBE=∠CDB=25°,
∠CAE=∠CDB=∠CBE=25°;
(2)∵∠CFE既是△AEF的外角又是△BCF的外角,
∴∠CFE=∠CAE+∠AEF=∠CBF+∠FCB,
∵∠CAE=∠CBE,
∴∠AEB=∠ACB=90°,
∴AE2+BE2=AB2,
∵∠ACB=90°,CA=CB,AC=5,
∴AB2=AC2+BC2=50,
∴AE2+BE2=AB2=AC2+BC2=50.
点评 本题考查的是轴对称的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
相关题目
14.某广告公司欲招聘广告策划人员一名,对A,B两名候选人进行了三项素质测试,他们的各项测试成绩如表所示:根据实际需要,公司将创新、综合和语言三项测试得分按4:3:1的比例确定两人的测试成绩,此时谁将被录用?
| 测试项目 | 测试成绩/分 | |
| A | B | |
| 创新 | 85 | 70 |
| 综合知识 | 50 | 80 |
| 语言 | 88 | 75 |
19.春节将至,某移动公司计划推出两种新的计费方式,如下表所示:
请解决以下两个问题:(通话时间为正整数)
(1)若本地通话100分钟,按方式一需交费多少元?按方式二需交费多少元?
(2)对于某月本地通话,当通话多长时间时,按两种计费方式的收费一样多?
| 方式1 | 方式2 | |
| 月租费 | 30元/月 | 0 |
| 本地通话费 | 0.20元/分钟 | 0.40元/分钟 |
(1)若本地通话100分钟,按方式一需交费多少元?按方式二需交费多少元?
(2)对于某月本地通话,当通话多长时间时,按两种计费方式的收费一样多?
 如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和等边△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:
如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和等边△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:
 已知,如图,点A、B、C、D在一条直线上,AB=CD,EA∥FB,EC∥FD,求证:EA=FB.
已知,如图,点A、B、C、D在一条直线上,AB=CD,EA∥FB,EC∥FD,求证:EA=FB. 已知:当x>0时,反比例函数y1=$\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A、B.
已知:当x>0时,反比例函数y1=$\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A、B.